不得不说，有时候无知是福，看到一点有趣而深刻的东东，就能感觉到神奇。越是我们熟悉的东西，往往却是我们进一步理解深刻的障碍，而之所以是障碍是我们并不知道这个是我们理解问题的障碍。困惑中的每一次豁然开朗往往是从一点一滴的我们已经成为惯性思维中开始。越是深刻的原理，往往越是简单强大。就像爱因斯坦打破牛顿给我们原有的世界观一样。对于一个打破常规，让你重新理解问题的最简单的方法就是把你整个思考的前提否定。而带来的结果就是我们看问题的角度，层面有了更大的扩展。所以，有时候知道的太多反而不美，做一个白痴也很幸福。

哎，又无病呻吟了半天。之所以有上述感想。还得感谢自己的同学。由于我没有看过MIT的经典课程《算法导论》而被鄙视，而且更无语的是，我的理由是“听不懂，如果有老师的课堂发音的记录”，而事实上。这个MIT早就提供了，为了照顾想我这样的听力不好的家伙。好吧，我是个白痴，不过就像上面讲的，白痴也有白痴的幸福。这个假期，无聊的时候，不仅可以看《爱情公寓2》也可以屡屡自己的数学常识了。：）

《算法导论》是一名研究算法设计的课程。设计算法，我们关心的主要是2个方面，一个是性能，另一个是资源花费。当然，我们重点的是性能，我们总是希望我们的程序跑的更快。那么学习算法到底有什么用呢？这是一个经典的问题。Charles Leiserson 是这样给我们解答的。首先，列举了一大堆在实际编程中比性能更重要的东西：可维护性，模块化，功能，用户体验等等。特别是用户体验，那么既然有这么多的东东比算法重要，那么为什么我们还要学习算法呢？

算法决定了可行还是不可行。

在一些实时的情况下，比如机器人等嵌入式设备，我们不够快，那么就没有意义，如果我们用了太多的内存，同样不行。所以，算法这个东东，总是在我们计算机领域的最前沿部分，如人工智能，搜索引擎，数据挖掘。如果我们是在做10年前就已经实现了的东西，那么性能的确在一些情况下已经不重要了。但是，如果想做一些别人没有做过的东西，真正的实现从无到有的过程。那么其中遇到的绝大多数问题都是，数据太复杂了。没有能力在有限的资源下找到答案。这也就是为什么叫计算机科学，而不是计算机工程。（当然科学这个和名字是无关的，比如物理，从来没有那个学校叫个什么物理科学什么的。：））。不得不说，MIT的目标是为世界培养leader，而我们那破学校是为了培养farmer（这里并没有不敬在里面，而且事实上，做一个farmer挺好的，每年坐在家里，收个房租，年末村里再分个几十万，比那些城里白领好多了在物质上）。其实也不那么绝对，非要改变世界，只要是之前没有做过的程序，我们在实现之前，首先思考的一定是算法。其次，则是对他不断的优化，完善。

对绝大多数的刚刚参加工作的同学，往往不能体会到整个产品的创建过程。参与的仅仅是完善，算法的设计或是大体设计已经完成，所以感觉不到算法的存在。而匆匆下了学校白学的定论。而随着工作时间变长，总会遇到没有或是不能直接利用原有设计的东东，那么算法也就体现出价值了。

算法是一种描述程序行为的通用语言。

我们可以通过算法去描述程序的运行流程，在任何地方。他不仅能在实践中得到体现，也能在理论中得到证明。而且能够得到大家一致的看法。而这是别的永远无法做到的，比如用户体验，每个人都有自己的想法，我们不可能让所有人都满意我们的设计，而算法却可以做到，因为快就是快。放到计算机上一跑结果自知。别人无法击败你，即便是再挑剔的对手，只要你足够出色。而能够满足这样条件的前提就是，算法是一个如此一般化，基础的东西。就像Charles Leiserson 所讲，算法就像钱，你可以用钱去买吃的，喝的。而衡量这些花费的就是钱的数目。在计算机上，则是，选择一个这样的策略，需要花费多少。选择另一个策略，需要花费多少。而衡量这2个选择谁的花费多呢？是算法。

算法在计算机中的地位，就和数学在所有理科学科中的地位一样。我曾经问过我的数学老师一个问题，他的回答让我直到现在还记忆犹新。“老师，数学在您眼中是什么呢？”“数学是所有理科中是最奇妙的一个。因为他可以独立于其他任何学科存在而其他学科离开不了数学。”是的。能够想象物理化学离开数学之后是什么样子么？但是数学为什么能够独立存在？是因为他构建了一门语言，一门伟大的语言。使用这门语言可以让知识在任何领域中环绕，学好数学就好像有了一张无限透支的通用支票，可以在任何地方花费（黄金？）。作为一个可以让这么多地方都通用的原因中最重要的就是，他是超级稳定的。是一个说一不二的世界。一个公平的世界，绝对的世界（当然，现在数学这个概念也不准确了，这个充分体现了哲学思想，有正必有反啊：P）。他所确定的东西的结果是肯定的。没有歧义，而且不随时间变化而流动。比如，我们真实世界中交流的语言，比如“忽悠”，“猥琐”。等等。很多词义，随着时间的变化而改变了。使得很多年纪大的人，和我们这年轻人在交流上就产生了隔阂。而我们最熟悉另一个例子就是文言文，特别是其中的一些扭曲的字。但数学这种基础类学科是不会的。至少在一个可以预见的范围是稳定的，没有地域限制的。所以，数学才能站在人类科学发展的最前沿，他的每一次前进的一小步，都能改变世界。这就是数学之美。同样也是自己能够让绝大多数人接受的最大障碍。由于他改变的太慢，而且枯燥。绝大多数人无法深入的理解。当用世俗，腐烂，充满铜臭，功利的眼光看待纯净的数学世界，必然发现数学无用。而且，这的确是事实，因为大部分人，都不可能成为改变世界的家伙（这里的确不准确，因为改变世界话题太大，修理地球同样也是改变世界。）。

算法，同样为我们计算机构建了一个纯净的世界。一个说一不二的世界，他所确定的，没有能够反驳的。当然，就和学习数学一样，我们不是去成为数学家，学习物理，不是去成为物理学家，然后去做哪些能够改变世界的东西。学习这些基础类学科的重要在于，他提供了一个让我们和那些站在人类史上最顶尖的家伙们交流的语言，从我的角度来看。如果没学好数学，能够和牛顿，爱因斯坦交流么？没有学好算法，能够和高爷爷交流么？作为一个普通人，我们只要学习到他们身上的一点点，也就足够了。当然，这不是对所有家伙都有效，有些人总是想，和那些老家伙有什么好交流的，给我一个周杰伦的签名吧。：）

学习算法还有一个原因，是的，就是兴趣。这个传说中最牛X的老师。

喜欢算法，没有别的原因，是的。我就是喜欢比别人快速的感觉。喜欢数学，是的。因为大部分人数学不好。所以我就喜欢数学。迎难而上，哥就是喜欢做别人做不了的东西。是的，虽然听上去很牵强，而且比较扭曲。比较符合印象中90后的想法。不知道90后是不是能产生更多的数学家呢？

让我们回到我们的算法上，既然我们这么关注性能，那么什么是影响性能的因素呢？

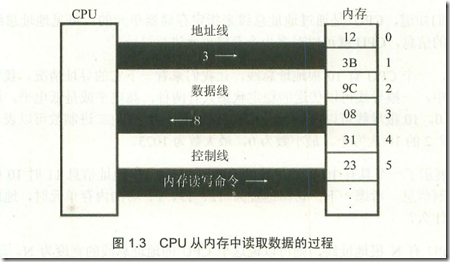
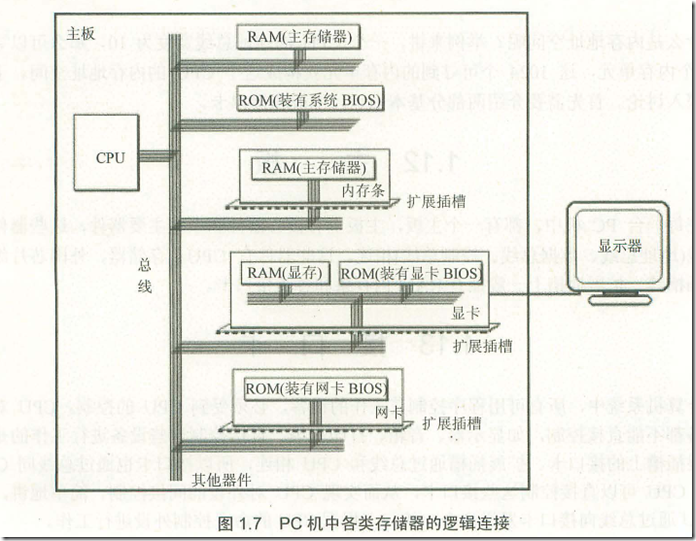
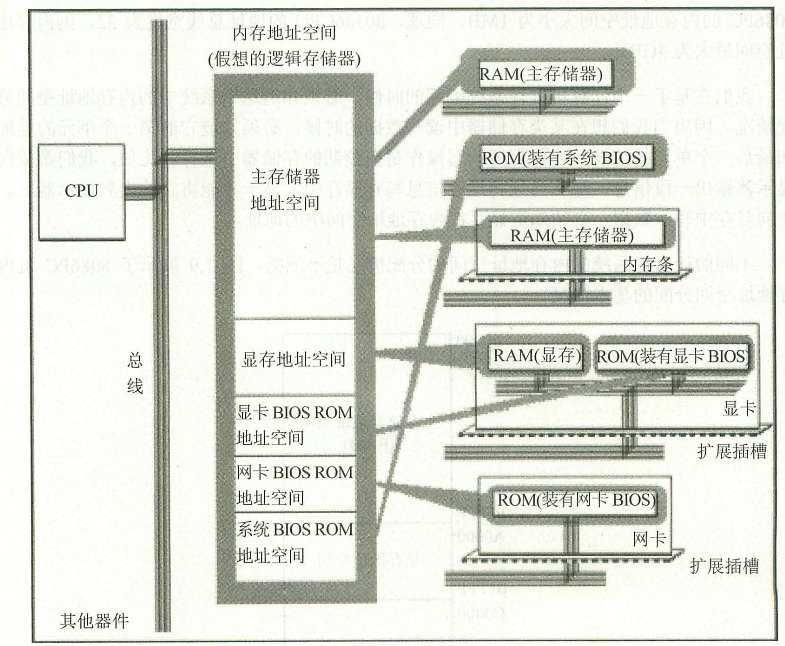
对于一个计算机外行来说，首先就是计算机硬件本身的运算能力。多一个超级牛的CPU，超大的内存，固态硬盘。肯定运算快。的确，如果你拿一个超级计算机和地摊上买的一个小的计算器比运算能力。这个实在是一个很显然的结果。是的，所以，我们有些情况下，需要思考在相同条件下，到底哪个算法的性能更高。这比较的是相对速度。但是我们却不能忘了这一点。有时，我们想使用一些很一般的计算机，通过优秀的算法，来打败那些拥有更高硬件的那些家伙们，而我们则必须关心算法性能的绝对速度。那么我们该如何描述这些看似互相矛盾的东西呢？不要忘记，算法可是基础啊，我们要的是一个确切的答案。我们如何给出一个确切的答案，而这个答案不管是超级计算机，还是普通PC都能够支持呢？这就是算法中最重要的一个概念，甚至是一切分析的大前提，一个可以把这些复杂的因素都考虑在内（或是都不考虑在内）的东东转换为可以用数学分析的对象。这就是渐进分析。

渐进分析的基本思想是

忽略硬件结构

不使用真实世界的运行时间，而是关心运行时间的增长速度为对象

渐进分析是一个非常庞大的概念，我们最熟悉的，也是大多数本科院校教我们的就是Θ,O,Ω等等类似的这些符号。这里只从Θ开始。

对一个初学者，Θ-notation是比较容易接受的。对一个多项式，我们只需要删除掉所有的低次幂项，忽略掉常数，系数这些次要因素。就和Charles Leiserson 所讲的。这个描述，是工程方向的描述，并不是严格的数学上的定义。而对像我这样的小白来说，最大的误解就是把他当成了数学上的严格定义而产生了极大的困惑。

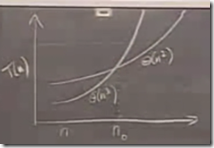
这个是一个相当经典的图，当n趋于无穷大时，Θ（n3）总能干掉Θ（n2）。不管是同样的硬件设备，还是不同的硬件设备。只是在不同的设备下，不同的算法下，我们有了一个不同的系数，低次幂项，和常数。但是，我们关心的是他随着数据输入长度的变大而产生的增速。当n超过n0时，任何的次要因素都是浮云了。我们就可以说Θ（n3）被Θ（n2）干掉了，即使Θ（n3）的硬件要比Θ（n2）好很多，在一开始的时候效率有多高。

这是一个伟大，cool的概念。是的，他完美的既满足了我们追求的绝对速度，也能满足我们追求的相对速度。可以说，这给了我们继续学习算法的动力。但是，事实上，在实际开发中，我们有时候却使用那些在学校中认为是效率低的算法。难道这个理论错了？当然不是，错的是我们，我们忽略了一个很大的前提，n0。在我们多数开发过程中，很少接触那些海量数据的运算。我们的运算多数是在一个较少的数据上下浮动，这个也可以说我们的硬件，资金，产品，根本不需要我们整那么大的数据。也就是n0，我们根本达不到。事实上，只要是有脑子的，看到这个图，在小于n0的前提下，都会做成正确的判断。但对于刚刚步入IT的广大学生，却总是犯下屁股决定脑袋这样愚蠢的选择。而这其实，就是做科学和做工程师的最大区别。理论和实践相互掰手腕的结果。

这几天，挖老赵的“坟”，找出了这么一篇。写程序时该追求什么，什么是次要的？里面有一段十分搞笑的代码，之所以这样说，是因为我自己也写过这样的代码。想想真是dt啊。回想事发现场，我记得是我看了个什么类似《面试宝典》东东，有一些题考察交换元素，事实上，你可以找到一大堆的，而且是更精妙的去交换2个元素。看到之后，如获至宝。只要是2个元素要换位置，就用。站在做科学的角度上看，这无可厚非。但是如果站在工程的角度来看。这就是明显的画蛇添足。往往花费80%的精力在提高%20的性能上，而不是去花费20%的精力提高80%的性能。这同样是刚刚步入IT的广大同学的问题。做科学需要严谨，但是在工程方面，考虑的事情非常复杂，多。我们必须要关注在核心，关键的部分。这样才能在有限的资源下，最大的做出东东来。实践中，没有任何项目的资源是足够的。MS，Google都会有资源不足的时候。我们需要学会抓住重点。当然这里并没有鄙视这些面试问题，事实上，这些问题的背后往往是考察数学思维的基本功，而不是鼓励大家这么做。就像那个经典的问题，12个小球一架天平。没有仔细，严谨的思考，能够想到这个东东能和排序问题扯上勾么？神啊，万恶的功利，给完美的数学模型批了一层邪恶的外套，使我们在追求本质的过程中迷失。

有关n0的问题，不仅在算法设计上，也出现在我们的设计模式之中。《设计模式》这本神书，我是没看过，也不敢看。但也隐隐感觉到类似“设计过度”的言论。这同样都是在理论和实践结合上出了问题。当然，不少理论支持者，肯定会说，那是因为你没做过那么大的项目。但事实却是，不管设计多么复杂的，还是多么简单的，实践和理论永远不可能都得到满足。windows操作系统可以说是一个我们可见的最大的项目之一了。但是windows也并不是一个微内核，在内核中也绑定了非常多的“多余”的部分从理论上看。那无疑会降低系统稳定性，提高维护难度。但是我们却不能不说windows是最成功的一套软件之一（这个之一甚至都可以去掉）。

当然，要想在做学问和实践找到平衡点。这个无疑是极大的挑战。只是分析理论，而不实践，那么永远不可能成为一个出色的工程师。除非你的目标是成为理论科学家。反过来，如果不理论而只是实践，不同的是，这个是可以成为一个出色的工程师。所以，这里有一句经典的话。

If you want to be a good programmer, you just program ever day for two years, you will be an excellent programmer. If you want to be a world-class programmer, you can program every day for ten years, or you can program every day for two years and take an algorithms class.

既然算法是如此的重要，那么我们该如何学呢？其实，这是一个很纠结的问题。甚至是一个鸡生蛋，蛋生鸡的问题。不学算法，你不会了解他，也不会认识到算法重要，反而。认为算法不重要，那么也就不会下功夫去学。这就又回到一开始的那个unknown unknown上了。所以，如果准备学习算法，也就意味着选择了一条坎坷的路。一开始特别迷茫，但是没有别的选择。唯有坚持，放下浮躁，功利的心态，沉浸在数学的世界中才能体会到数学的价值，数学的乐趣。也只有这样，才能坚持到最后。

当然，能做到这一点的，敢说体会到数学之美的家伙，全世界也没有几个人。那么作为一个普通人，我们怎么才能最大的去提高自己，更好的掌握实践和科学的平衡点呢？这个问题，我自己也没有答案。因为我既没经验又没理论。这里只是扯下我自己的理解，可能很偏激。

首先应该研究下刘未鹏的很多博客内容，特别是锤子和钉子。对我这样的新手来说，武器真的太少了。所以当捡到一个武器往往过于兴奋而忽视了这个武器的使用前提，往往杀鸡用牛刀，而且还达不到积极的效果。就是因为我们拿到锤子之后，所有东西看上去都像钉子。所以，我们唯有摆正心态，深入了解拥有的武器，并增加更多的武器，见更多的市面，才能坐怀不乱，达到手中有锤，心中无锤的最终境界。

一个稍微实际的例子。对像我这样的菜鸟来讲，大部分都会遇到这样一个问题。而且困惑很久很久。“堆排序为什么比快速排序在大多数时要慢呢？”事实上，造成这个问题的主要原因（对我）就是，没有理解明白Θ-notation。那些被忽略掉的次要因素，当然还有更重要的是数学上对概率的薄弱理解。然后我们会再映射出一大堆的数学基础知识，然后大部分人死在沙滩上（真的，这是我从小以来最大的遗憾，就是没有学好概率，而造成这个的原因居然是，这些题目初学时往往是用日常用语出题，而由于本人语文太差，总不能理解清楚题意，而对这类题目产生了极大的抵触，可见小朋友们千万不要偏科:P）。从科学的角度去，完全可以证明这个问题，但是付出的代价就是没有硕士以上的数学能力的玩家，没有机会理解到那个层次。那么，其实我们可以从另一个角度看，直接放到计算机上跑一下就可以了么。是的，我不是科学家，我只需要知道结果就OK了。是啊，好在我们处在一个和谐的世界。让我们从这个庞然大物中得以解脱，所以，有时，我们需要根据自身情况，放弃一些东西，特别是那些比较能够通过实验来证明的东西。

好吧，总不能啥也放弃吧，都放弃了那到底也简单了。这里，我只能说，我推荐SGI STL。在我看来，这是一个结合了设计模式，理论算法与实践最好的一个实例。他不仅是开源的，代码量也不多，命名也算规范，而且还有一本侯捷大师的著作来诠释，帮助我们理解，而且还能帮助我们具体实践过程中规避一些错误。我们每一个在学校学习的算法，我们都可以在这里找到答案（至少可以用来做作业拿高分对某些特别的女生），而且都会比一般大学讲的深刻，事实上，我认为，大学现在的教育为什么觉得无用，不是太难太理论，而是教的太简单了，简单到已经没有用的地步了，从而根本没有实际意义。（大学联合培训机构，是我所见过的，比大学扩招还要搞笑的事情）比如快速排序，SGI STL做了非常多的优化来保证无论在什么时候，都不会退化到n2，在分的过程总是分不好时，采用堆排序。在快速排序到做最后几步，为了减少开销而采用插入排序去做哪些马上就要排好序的部分。而这些策略，并不是凭空想象，都可以在高爷爷的著作中找到理论证明，以及网上的各种论文，前提是你的数学功底足够（当然这里实践在前还是理论在前这个实在是没有讨论的意义）。所以，理论不是没有用，只是自己学的太肤浅。实践也不是没有用，只是自己没有考虑那么多的情况，想的太简单而已。

当然，这个可能又会引起另一个庞大的问题，“不要重复制作轮子”，不过这个已经大大超出这篇文章的范围了。我自己的看法是，STL是为了实现最基本的最通用的东东的，而实际过程中，我们往往有自己的特殊性。而这些特殊性是STL不可能设计时都给我们考虑周全的。也就是我们很可能需要扩展，重写部分以适合我们的需要。当然，现在离这些目标还很远很远很远。

操作系统是连接硬件和应用软件之间的纽带。至少目前是这样的。而操作系统这门课也是计算机专业的必修课之一。无奈当时混沌。并没有真正的上好这一门课，之所以叫胡言乱语。是因为这里面的水对我来说实在是太深了。任何一个小的问题背后都是一个深渊。所以第一篇，从最初的（大学课程最初）开始讲起。

8086，应该是学计算机最开始的地方。可以说是我们现在x86系列的最简单，最基础的实现。里面的设计都或多或少的影响到了后面系列的实现。所以，学校从这里开始，的确是非常明智的，虽然当时我不这么认为。但是想要了解或是明白8086的设计，那么也就要带出另外的那些更为底层的，计算机指令集，机器语言，引脚，门，电压等等。当然我不是说这些不重要，但是如果有这些基础，的确可以加快，加深8086以及其他系列的一些知识的理解。这里就略过这些东西。一是自己能力不足，二是我觉得现在谈这个真的不是很重要。想想，这2个原因其实也就一个 ：)。

存储器是计算机的核心部件。现在的计算机围绕存储器来构建，所以必须从存储器开始。

在CPU眼中，存储器保存的东东。只有2种：指令和数据。当然退而求其次，存储器中没有指令和数据之分，只有0和1。这个世界的确是非常的和谐简单。那么CPU是如何分别这2种东东呢。这完全取决于CPU自己。当遇到二进制信息如1000100111011000时，CPU可以把他看成大小为89D8H的数据处理，也可以看做是指令mov ax bx来执行。

存储器被划分为若干个存储单元，一般来说，一个存储单元大小为一个Byte。一个拥有128个存储单元的存储器。容量为128个字节。

那么存储器被划分为了多个存储单元，从0开始排序。CPU从内存中读取数据，首先需要的就是存储单元的地址，也就是CPU需要知道读取哪一个存储单元中数据。当然CPU不仅仅需要知道地址，还需要告诉存储器要做什么操作，是读还是写？而且在计算机中，也不仅仅只有一个存储器，也不仅仅只有一种设备需要去操作。还需要指明对哪一个设备操作。所以。CPU对数据的读写，需要以下的基本信息。

存储单元地址（地址） 设备选择，读写命令（控制） 读写的数据（数据） 那么CPU通过什么来将这些信息传递给设备呢？CPU计算机中的这些设备处理传输信息都是电信号,连接这些设备的导线为总线。总线根据传送信息不同，分为地址总线，控制总线，数据总线。

CPU从3号单元中读取数据过程：

CPU通过地址线将地址信息3发出 CPU通过控制线发出读命令，选中存储器，通知到读数据 将3号单元中的数据8通过数据线交给CPU 既然知道了CPU读取数据的流程，那么CPU能够找到多少个这样的地址是我们遇到的下面的问题。显然，地址总线上能传递多少种不同的地址，那么CPU就可以找到多少个存储单元的地址。

如果CPU有10根地址总线，1根能够提供2种信号：1、0。那么10根就能提供2^{10个，也就是1024种。那么我们就说CPU的寻址大小为1K。或这个CPU的地址空间为1K。}

CPU与各个设备之间传递数据是通过数据总线进行。所以，数据总线的宽度决定了CPU和外界数据传递的速度。我们很容易想到16根数据线可以一次传递2个字节。

同样类似的。控制总线的宽度，也决定了CPU对外部的控制种类。所以，决定了CPU对外部的控制能力。

当我们买电脑的时候。除了考虑CPU以外，还需要搞定一个好的主板。当我们打开电脑之后，看到的首先也是这个大家伙。而且如果你的电脑主板被烧坏的话，那么基本上这个电脑主机也就完蛋了。可见主板在现在计算机中的地位。

主板最基本的作用就是通过它把计算机的核心部分通过总线（地址、控制、数据总线）相连，并且还需要为扩展预留接口。当我们买到一个主板时，会看到有非常多的接口卡槽，而事实上CPU控制这些设备就是通过总线去控制这些接口卡来进行的。

上面的那些东东，不管是显卡，声卡，网卡。都有两点相同。

都和CPU总线相连 CPU进行读写操作是，都是通过控制线发出内存读写命令。 也就是说，CPU操作他们的时候，都把他们当做内存来对待。把这些不同的设备组成一个大的逻辑存储器。这个逻辑存储器就是我们的地址空间。

在上面这个图中，所有的物理存储器都被看作一个由许多存储单元构成的逻辑存储器，每一个都有一个地址段，也就是一段地址空间。CPU往这段空间中读写数据，其实就是读写了物理存储器。

那么我们可以看出。CPU的地址总线宽度是在是太重要了。在我们的8086中，地址总线宽度为20，也就是可以搞定2^{20个不同的地址。也就是说8086的地址空间大小为1MB。}

不同的计算机系统，的地址空间分配是不同的。如下是8086的

看到这幅图，那么我们就可以从容的写一个HelloWorld程序输出到我们的屏幕上。

因为我们可以直接在A0000~BFFFF中写数据，而这些数据会跑到显卡中最后跑到屏幕上。

那么我们现在明白了。CPU访问内存单元时，需要给出这个内存单元的地址，所有的内存单元构成存储空间是一个一维线性空间。每一个内存单元在这个空间中都有唯一地址，这个唯一的地址，就是物理地址。

CPU通过地址总线送入存储器的。必须是一个内存单元的物理地址。同样，这个地址在CPU内部中必须搞定这个地址，再发送到地址总线之前。不同的CPU形成物理地址的方式也不同。而我们现在所考虑的就是8086是如何搞定这个物理地址的。

那么我们又必须要了解些其他知识。8086是16位结构的CPU。那么他的意思是

运算器一次最多处理16为数据 寄存器最大宽度16位 寄存器和运算器之间的内部线为16位。 也就是说，8086一次只能处理，传输，存储（寄存器）16位的地址。从我们大多数人的思维，一个地址，也就是一个指针，最好和一个整数的长度一致。但是，我们知道8086的地址总线为20位。达到了1MB的寻址。为什么会是这样的呢？在很久很久以前，当CPU的技术从8位发展到16位的时候，地址总线本来也应该是16位，也就是64K。但是大家发现这个太小了。然后intel决定采用1M。这个在当时，的确是非常的大，而盖茨甚至还有“无论对谁来说,640K内存都足够了”的言论。当然。这里并没有不敬在里面。只能说，计算机的发展实在是太迅速了。所以，地址总线的宽度为20位。但是这个带来了一个问题。面对16位的ALU，如何来填补这个呢？

Intel设计了一种在当时看来一个非常巧妙的方法。也就有了我们现在看到的8086地址翻译。16位段地址+16位偏移来形成这个20位的地址。

随着计算机的发展，我们越来越的希望计算机能够处理更多的事情，伴随着CPU运算能力的提升。整个计算机的性能主要是卡在了CPU利用率上。面对“优秀”的CPU，我们并没有充分的利用它实在是暴殄天物。所以我们希望我们的CPU能够给我们做更多的事情，最好不要停。就像老早的资本家总是希望工人天天干活一样。

不幸的是，在当时的DOS操作系统下面。是单任务的。并不支持多任务。我们不能在听音乐的时候打开文本文档编辑。那么，构造计算机的那些老前辈们，想到的一个招数是时间片。每个程序都有机会获得这些时间片，通过不断的轮询，只要这个时间足够短，那么人类是无法觉察出来。我们会有这个错觉，好多的程序再一起执行。

虽然我们在DOS可以利用内存驻留的技术实现类似的体验，但是这个却并不是安全的。因为我们往往是通过修改中断向量表来做。我们无法保证其他程序是否正确修改中断向量表。而且如果我们的程序通过这里修改，并成为我们程序的一部分时，也就意味着，其他的程序也能这么做。那么我们很难保证计算机中的各个程序能够互不影响。同样，包括操作系统。这也就意味着我们无法构建一个安全的环境，让我们的操作系统，以及各个程序不互相影响，制约。

同样，当我们将CPU时间片分给那些程序的时候。在一开始的初期，并不是我们这样的多任务。而是一种叫做协作式多任务。操作系统控制CPU的时间片，而每个程序形成一个队列。每个程序在获得CPU时间后必须归还CPU。注意，这里的归还是程序本身的事情，而不是操作系统的事情。也就是说，如果有一个程序不想归还时间片，或是他不小心陷入一个死循环，那么别的程序也就无法执行，甚至包括操作系统自己本身。因为他自己也在那个队列里面傻等。那么这整个世界也就变得混沌不堪了。因为操作系统，并不能识别哪一个程序是不良的程序。

造成这些问题的根本原因在于，我们并没有等级的概念。也就是说，整个硬件资源对我们的每一个程序都是平等的。事实上8086下我们看到了任何一个程序，都可以通过段+偏移来实现访问整个地址空间。甚至是中断向量表还有硬件。所以，在这个原始社会下。我们达到了真正意义上的公平，但是也验证了低下生产力的现实。

所以，为了实现这些功能。必须有硬件的支持。那么80386也就跳入了我们的视野。事实上，他就是为了支持我们的想法（实现多任务，实现各个任务互不影响）而诞生的。

在开始介绍80386之前。我们好好思考一下我们需要实现的功能。

实现等级观念，有些程序需要有特权。执行一些系统的核心部分，而一些程序必须在一些限制上运行。具体的讲则是有些地址空间不能访问，有些寄存器不能读取或是修改。 需要提供一个复杂的内存管理，来帮助我们实现各个任务的独立的地址空间。这样可以保证一个任务不会随意修改另一个任务的数据。 其实，让我们说到根上。其实我们需要实现针对地址空间的保护。只有实现了这种保护机制，我们才能保护操作系统的代码，维护操作系统的特权。而有了操作系统的支持下，我们才能继续去谈内存管理，和保护操作系统之上的各种程序之间不互相影响。搞定了这些之后，我们就不难理解8086的缺陷以及80386为什么要实现这些功能了。当然。这个过程肯定不会像8086那样平滑。因为这完全是一个不同的设计思路，思想。即使，他披着一张似乎有着段加偏移量的一层皮。

好吧，让我扯的远一点。随着生产力的发展，有一个超牛B的程序，他想做其他程序的老大。让他们乖乖听话。而这个程序，就是操作系统。可惜啊，在原始社会，生产力不足。并不能让所有的人都听话。让我们暂时告别原始社会，我们来到了奴隶社会。其实计算机发展也和人类社会一样。我们出现了阶级，让我们仔细看看这个维持统治阶级工具的核心——80386体系结构。

80386以后，CPU历经多种改进，虽然速度提高了几个量级，功能上也有很多改进。但并没有重大的质的改变。所以统称为i386结构，如果除去大量的3D密集型图形图像运算，并行等之后。其实，只是相当于一个更更快速80386而已。

80386是32位的CPU。也就是ALU数据总线是32位。这里，我们终于在地址总线和数据总线一致了。都是32位。当面对地址总线的宽度达到32位。也就是CPU的寻址能力达到了2³² = 4G。这的确是一个相当大的空间。为了保证这个空间的和谐。80386增加了一个叫做保护模式的一个名词。但是为了和之前的8086体系兼容，又有了实模式和虚拟86模式。

这里只是简单的介绍。实模式，没有什么其他的意义。只是比原来的8086寄存器大了。CPU快了。一些指令和操作更加方便容易了。

保护模式则是重点。事实上，没有保护模式，现代操作系统是无法构建的，在x86下。

既然我们有了这么大的一个空间，那么该如何分配呢？很容易的想法是，我们可以把地址空间平均分给各个任务。那么他们都有了各自的地址，他们只要在各自地方做就好了。但是这个同样假设这各个程序都是善良的。而且，对于各种各样的硬件又该如何做呢？他们所映射的CPU地址空间该如何保护？而且，当我们真正的运行着相当多的任务的时候，我们的内存，是否还能经得住呢？而这些问题归根到底是因为CPU的地址空间每一个任务都是可见的，那么就想通过各种各样的渠道来搞破坏。所以，为了构建操作系统的核心地位，以及各个任务之间的互不干涉。操作系统中最重要的概念登场了——虚拟存储技术。

其实，这是一个很简单的道理。统治阶级（操作系统）为了维持他的权威，他把珍贵的核心资源（CPU地址空间）和被统治阶级（用户程序）之间加了一个中间层，从而核心资源（CPU地址空间）对被统治阶级（用户程序）是透明的而统治阶级（操作系统）所独占。然后他又对所有的被统治阶级（用户程序）整了一个弥天大谎:“你们有整个4G的CPU地址空间。而且你们在跑的时候（程序运行）是独占所有资源的”。然后被统治阶级（用户程序）就在这个统治阶级（操作系统）下勾画的这个美丽的世界下安分的生活下去了，至少是绝大多数。（这里的表达不准确，这里的用户程序，其实我的意思是任务，或是说，在普通程序，我们可以写这么一个地址，在高地址空间上，只是如果我们去操作他，操作系统不让我们这么做。但是我们还是能“看”到的。感觉还是不合适，这段可以去掉：)）

OK。操作系统给这个世界整个一个这么大的谎言。现在计算机的核心资源都在他的掌握下了，他的目的终于达到了。但是就和再苛刻的资本家也得给工人发工资一样。如果没有了被统治阶级，统治阶级还有什么存在意义呢？所以，操作系统也必须给用户程序一个高效的获得CPU资源的方式。也就是要给用户程序发工资。

而一个程序运行的最基本的要求就是数据。瞎话扯了这么多。该来点正经东东了。

80386CPU的内存管理支持2种，段式，和段页式。这些都为操作系统实现内存管理提供了硬件基础。

CPU的段机制，提供了一种手段。可以将系统的内存空间分成一个个较少的受保护区域。每个区域称为一个段。每个段都有自己的基地址，边界和访问权限。但是80386在实现这个的时候，不得不背上历史的负担。intel选择了在原有段寄存器的基础上构筑保护模式。并保留了原来的16位段寄存器。并添加了2个段寄存器FS,GS。但是我们看到了。光是用段寄存器来确定一个地址是不行的。因为我们需要这个地址段的长度（边界），访问权限等等。所以，这里变成了一个数据结构，而不是之前8086的那个单纯的基地址。

所以，intel在做这个的时候，改变了段寄存器的功能，使他从单一的基地址，改成了指向一个数据结构的地址（或是数据结构的指针可能好听点）。这样，CPU才能获得它足够的信息。而这，也是学过8086 再看80386最让人迷惑的地方。因为这个完全是2套东东。而且根本上没有任何关系。

让我们捋一下当一条访问内存指令的执行情况。

根据指令的性质确定使用哪一个段寄存器。 根据段寄存器内容，找到相应的段描述符结构。 找到基地址。 将指令中的发出的地址位移，检查是否越界。 根据指令的性质和段描述符中的访问权限看时候越权。 一切正常，我们相加获得实际物理地址。 CPU搞定段需要知道3个信息。

段基地址 段界限 段属性 段信息的长度是64位。段基地址32位。段界限20位，段属性12位。而这个段信息标准的叫法就是段描述符。而许许多多的段描述符组成个段描述符表。

为了能够访问段描述符表，80386中新增了2个寄存器来寻址段描述符表：GDTR和LDTR。GDTR为全局描述符表寄存器，LDTR为局部描述符表寄存器。GDTR是48位，直接指向内存的线性地址，32位的线性基地址，16位的边界描述这个表的大小。LDTR是16位寄存器，表示的是全局描述符表的索引。这说明LDT其实就是GDT中的一项而已。

段寄存器中的内容为16位。由于指向的内容改变了。所以也有了新的名字，为段选择子。

TI表示要索引的段描述表种类。TI = 0表示全局描述符表，TI = 1表示局部描述符表。由于索引只有13位，也就是说，我们的表项最多2¹³ = 8K个描述符。RPL 表示请求特权级，用于特权检查。

我们现在仔细看看这个索引指向的内容，描述符表。

在一个多任务系统中。通常我们会同时存在很多个任务，每个任务涉及多个段，每个段都需要存放段描述符。那么描述符根据用途不同，IA-32处理器分为3种描述符表。全局描述符表GDT，局部描述符表LDT。中断描述符表IDT。IDT将放在后面中讨论。段描述符的结构比较纠结，充分体现了历史负担。这里也就不继续了，不过，这个真是一个相当“太监”的结构。

GDT表是全局的。一个系统中通常只有一个GDT。供所有任务使用。LDT和具体任务相关，每个任务都可以有一个LDT。也可以多个任务共享一个LDT。

根据上图，我们可以形象的看出，段内存管理的计算方式。讲了这么多的理论，让我们稍微动动手。

使用Windbg调试程序，可以使用dg命令来显示一个段选择子指向的段描述符详细信息。首先看下CS

Sel就是选择子（selector）。base limit就是之前的基地址，和边界。Code就是段的类型。RE = ReadOnly + Executable。Ac表示访问过

Pl表示特权级别（Privilege Level）。3的意思是用户特权。Size表示代码的长度，Bg意味32位代码。Gran表示粒度 Pg代表为内存页4K。Pres代表是否在内存中（我们之前看到了那么多的表项，8K，事实上并不是都在内存中的，当不在内存中时，访问会重新载入这个内容，所以需要记录）。Long 下的Nl表示 这个不是64位代码。

我们看到了SS DS ES 一样。

我们看到了类型是数据，并可以读写。而且我们发现。SS DS ES CS 的基地址都为0，长度都是整个内存空间大小。Intel把这种方式成为平坦模式（Flat）。我们看到了当我们通过段+偏移获得一个地址，其实基地址的作用已经没有了。limit也是最大空间4G，作用也很小了。可见，在平坦模式下，只是段管理的一个特例。我们只是关注与权限而已。

等等，少了一个。FS这个段寄存器比较特殊这里只是贴个图。具体的会在后面总结他。当然这里面的知识非常多，还有各种各样的段描述符存在。但是如果是和我一样在这些方面是新手，我觉得还是知道的少一点比较好。

我们看出，根据段内存管理下。我们把程序分成了不同类型。有代码部分，有数据部分等。但事实上，无论是windows 还是linux都没有采用段内存管理，准确说是只使用Flat模式,也就说。只是使用了权限部分来针对特权级对代码和数据保护。

Intel在80286实现保护模式，段式内存管理。但是发现了如果不支持页式管理是不行的。所以，在80386下，需要支持页式管理。也就是说，80386又背起了历史的负担，既要维护段式管理，还要实现页式管理。

之前的段式管理机制，是通过段寄存器转换加偏移形成一个32位的物理地址。这个是真正的物理地址，也就是这个是要在地址总线上跑的。也就是说应用程序获得的这个地址是真实的地址，那么也就对操作系统对内存换入换出增大了困难。而且对需要对code和data分类管理，导致程序加载过慢。而且缺乏足够的对内存管理的粒度，而究其原因，就在于它并没有真正的隔离用户程序和实际资源以及等等问题。所以，页式管理开始登场了。

本来页式管理和段式管理是不需要结合在一起的。但是在80386中。保护模式的实现是和段式管理分不开的（权限控制）。我们在查看CS的代码段描述符时，我们看出执行的这段代码的优先级是3。所以intel设计80386时，就考虑利用原有的基础再扩充。那么也就有了我们现在的基于段式管理的页式管理。也就意味着，我们需要在段式管理上再建立一个地址映射。说白了就是。这整个一套地址转译，需要将逻辑地址，通过段式管理转成线性地址，再通过页式管理最终转成真实的物理地址。那么如果我们启用了页式管理，那么段式管理的运行结果就不是之前的真实的物理地址，而成了一个中间地址或是线性地址。而这个过程。同样也是从8086跳到80386比较费劲的地方。

80386将线性地址空间划分为4KByte的页面（一般情况下）。每个页面可以被映射至物理存储空间中任意一块4KByte大小的区间。在段式管理下，连续的逻辑地址转译后在线性地址空间还是连续的。页式管理下物理空间却可以不连续。所以我们可控的粒度更小，从而更灵活。而物理空间的不连续，也就意味着我们可以更加灵活的把暂时不用的数据放到外部存储器，通常为硬盘。而这也就解决了我们多任务下，物理内存不够的情况。

当然，灵活的背后便是复杂的机制，在我们继续了解详细的页式管理过程之前。我们先看一下我们真正的需求，以及80386给我们提供了什么。

我们的首先目的是特权机制。通过特权机制来保证操作系统的权威。也就是一些指令，寄存器只能由操作系统这一级别的才能操作。而用户程序不能操作。这是段式管理已经搞定的。那么剩下的问题就是用户程序和用户程序之间互不影响。

在页式管理中，我们已经有了一个虚拟层：线性地址。事实上。每一个任务都有一个这样的虚拟地址。任务中针对地址的操作都是在这个虚拟地址上而不是真正的物理地址。我们知道。我们的数据最终和物理地址相关联才有意义。这个中间层，使得任务不知道自己确切的物理地址，也就为了保证一个任务不会被另一个任务随意修改或访问。

80386页式管理的核心是将线性地址空间划分成一个个页面，大小一般为4K。那么我们需要保存这一个个页面的映射关系。而我们知道，现在的地址空间大小是4G。那么我们剩下的就是如何管理，或是保存这些信息。我们首先发现，这个空间对我们绝大多数程序来说都太大了。所以为了减少保存这些映射的资源，80386使用了分级管理，所以，一个简单的线性地址被拆成了3个部分。

分别为Directory， Table 和Offset。

对于一般来说，页面大小为4K。为了能够找到每一个Byte，那么我们需要12位才能找到。也就是Offset = 12的原因。

我们称指向一个页面的地址（指针）为页表项，多个页表项的集合构成页表。10位table，也就意味着我们能够表示1K个pageTableEntry。那么我们总共能够表示的4MByte。

指向页表的地址（指针）为页目录项。多个页目录项的集合构成页目录。10位的Directory，也就意味着我们能够表示1K个Directory entry。那么我们总共能够表示4GByte。正好为我们的地址空间大小。

CR3寄存器，则给我们指出了Directory 的基地址。所以它又有了另一个名字，页目录基地址寄存器（PDBR）。

具体的取址这里就不描述了。因为上图已经很清楚了。

这真是一个看似完美的方案。但是现实是很残酷的。我们并没有那么多的内存。为了能够跑起那么多的程序，支持多任务，也就是意味着，我们需要在一些时候，把一些内存搬到硬盘。那么当我们访问这些页面的时候，就会产生pagefault，然后操作系统会把这部分页面再搬入到内存中。

当然，还有相当多的细节这里无法阐述。事实上，我们也不可能一下子把这些东东搞清楚，毕竟这些东西离我们还是有些远。下一篇将从应用的层面扯。当然在合适的时机，我们还需要回来。比如另一些重要的概念如中断。

SGI STL 在g++中默认的编译选项是构造2个分配器。

第一级分配器__malloc_alloc_template

这个一级分配器设计比较简单。由于SGI STL中分配内存没有使用C++推荐的 operator new/delete 而是使用malloc/delete。所以，并没有set_new_handler()。当面对内存不足的情况，这里模仿了c++的做法。

template <int __inst>
void (* __malloc_alloc_template<__inst>::__malloc_alloc_oom_handler)() = 0;

static void (* __set_malloc_handler(void (*__f)()))()
{
    void (* __old)() = __malloc_alloc_oom_handler;
    __malloc_alloc_oom_handler = __f;
    return(__old);
}

template <int __inst>
void*
__malloc_alloc_template<__inst>::_S_oom_malloc(size_t __n)
{
    void (* __my_malloc_handler)();
    void* __result;

    for (;;) {
       //这里不断的调用处理分配不足的情况代码，如果有可能解决问题，那么OK，如果还是不行，那么
         //只能抛出异常，当然，如果没有指定，默认为NULL，则会直接抛出异常。
        __my_malloc_handler = __malloc_alloc_oom_handler;
        if (0 == __my_malloc_handler) { __THROW_BAD_ALLOC; }
        (*__my_malloc_handler)();
        __result = malloc(__n);
        if (__result) return(__result);
    }
}

//这里，如果分配不足，则会调用_S_oom_malloc来救急。oom，就是out of memory的意思。
static void* allocate(size_t __n)
{
    void* __result = malloc(__n);
    if (0 == __result) __result = _S_oom_malloc(__n);
    return __result;

}

二级分配器 __default_alloc_template

二级配置器多了很多机制，在分配小的内存上做了优化。

粗略的分配策略。

分配大小超过 _MAX_BYTES = 128bytes，使用一级分配器处理。当分配器大小小于128bytes时，则通过内存池管理。 调整分配大小到8的倍数，从freeList中，分配内存。

template <bool threads, int inst>
class __default_alloc_template {

private:
  // Really we should use static const int x = N
  // instead of enum { x = N }, but few compilers accept the former.
# ifndef __SUNPRO_CC
    enum {_ALIGN = 8}; 
    enum {_MAX_BYTES = 128};
    enum {_NFREELISTS = _MAX_BYTES/_ALIGN}; //free_list 个数
# endif
  static size_t
  _S_round_up(size_t __bytes)
    { return (((__bytes) + _ALIGN-1) & ~(_ALIGN - 1)); }

__PRIVATE:
  union _Obj {
        union _Obj* _M_free_list_link;
        char _M_client_data[1];    /* The client sees this.        */
  };
//根据大小，找到对应的index，从1开始。
static  size_t _S_freelist_index(size_t __bytes) {
        return (((__bytes) + _ALIGN-1)/_ALIGN - 1);
}

可以看出，_Obj就是一个简单的单向链表，只是这个链表和我们之前学习的不一样。之前的链表数据只是链表节点的一部分，而这里当分配给client的时候是一整块的。

分配空间

static void* allocate(size_t __n)
  {
    _Obj* __VOLATILE* __my_free_list;
    _Obj* __RESTRICT __result;

    if (__n > (size_t) _MAX_BYTES) {
        return(malloc_alloc::allocate(__n));
    }
    __my_free_list = _S_free_list + _S_freelist_index(__n);
    // Acquire the lock here with a constructor call.
    // This ensures that it is released in exit or during stack
    // unwinding.
#ifndef _NOTHREADS
        /*REFERENCED*/
        _Lock __lock_instance;
#endif
    __result = *__my_free_list;
    if (__result == 0) { //没有找到freeList
        void* __r = _S_refill(_S_round_up(__n)); //这里重新填充 freeList
        return __r;
    }
    *__my_free_list = __result -> _M_free_list_link;
    return (__result);
  };

如果能够获得freeList，情况很简单，将__my_free_list 的值，指向已经分配空间的下一块空间。

/* Returns an object of size __n, and optionally adds to size __n free list.*/
/* We assume that __n is properly aligned.                                */
/* We hold the allocation lock.                                         */
template <bool __threads, int __inst>
void*
__default_alloc_template<__threads, __inst>::_S_refill(size_t __n)
{
    int __nobjs = 20;
     //由他来分配空间，第二个参数为引用， 所以有可能出现分配不足，也就是__nobjs < 20的情况。
    char* __chunk = _S_chunk_alloc(__n, __nobjs); 
    _Obj* __VOLATILE* __my_free_list;
    _Obj* __result;
    _Obj* __current_obj;
    _Obj* __next_obj;
    int __i;

    if (1 == __nobjs) return(__chunk); //如果只能分配一个大小，那么我们不需要调整freeList了。
    __my_free_list = _S_free_list + _S_freelist_index(__n);

    /* Build free list in chunk */ //构造freeList
      __result = (_Obj*)__chunk;
      *__my_free_list = __next_obj = (_Obj*)(__chunk + __n);
      for (__i = 1; ; __i++) { //从第二个开始构造freeList，因为第一个需要传给上层函数。
        __current_obj = __next_obj;
        __next_obj = (_Obj*)((char*)__next_obj + __n);
        if (__nobjs - 1 == __i) {
            __current_obj -> _M_free_list_link = 0;
            break;
        } else {
            __current_obj -> _M_free_list_link = __next_obj;
        }
      }
     //这里，我们发现，这个freeList，其实就是一个简单的单向链表，
    //__my_free_list = _S_free_list + _S_freelist_index(__n); 这个就是获得这个链表的表头。
    return(__result);
}

释放空间

/* __p may not be 0 */
  static void deallocate(void* __p, size_t __n)
  {
    _Obj* __q = (_Obj*)__p;
    _Obj* __VOLATILE* __my_free_list;

    if (__n > (size_t) _MAX_BYTES) {
        malloc_alloc::deallocate(__p, __n); //过大的block，我们通过1级分配器搞定
        return;
    }
    __my_free_list = _S_free_list + _S_freelist_index(__n);
    // acquire lock
#       ifndef _NOTHREADS
        /*REFERENCED*/
        _Lock __lock_instance;
#       endif /* _NOTHREADS */
     //这里是典型的在listHead 的下一个位置添加的操作，这里看出，对于小的block，我们并没有给操作系统，而是
    //链表保存起来。
    __q -> _M_free_list_link = *__my_free_list;
    *__my_free_list = __q;
    // lock is released here
  }

内存池分配

/* We allocate memory in large chunks in order to avoid fragmenting     */
/* the malloc heap too much.                                            */
/* We assume that size is properly aligned.                             */
/* We hold the allocation lock.                                         */
template <bool __threads, int __inst>
char*
__default_alloc_template<__threads, __inst>::_S_chunk_alloc(size_t __size,
                                                            int& __nobjs)
{
    char* __result;
    size_t __total_bytes = __size * __nobjs;
    size_t __bytes_left = _S_end_free - _S_start_free;

    if (__bytes_left >= __total_bytes) {
          //内存池足够，分配后返回
        __result = _S_start_free;
        _S_start_free += __total_bytes;
        return(__result);
    } else if (__bytes_left >= __size) {
          //内存池不够整个memory block，但是足够一个以上的block。
        __nobjs = (int)(__bytes_left/__size);
        __total_bytes = __size * __nobjs;
        __result = _S_start_free;
        _S_start_free += __total_bytes;
        return(__result);
    } else {
          //内存池已经一个都不能满足memory block
        size_t __bytes_to_get = 2 * __total_bytes + _S_round_up(_S_heap_size >> 4);
        // Try to make use of the left-over piece.
        if (__bytes_left > 0) {
               //内存池中还有剩余，找到这部分空间并填入相应的memory block list中。
            _Obj* __VOLATILE* __my_free_list =
                        _S_free_list + _S_freelist_index(__bytes_left);

            ((_Obj*)_S_start_free) -> _M_free_list_link = *__my_free_list;
            *__my_free_list = (_Obj*)_S_start_free;
        }
          //内存池为空，我们从heap中找内存
          //__bytes_to_get是一个不断增加的数字，也就是每次从heap分配的空间越来越多。
        _S_start_free = (char*)malloc(__bytes_to_get);  
        if (0 == _S_start_free) {
                //极端情况， heap的空间不足。
            size_t __i;
            _Obj* __VOLATILE* __my_free_list;
     _Obj* __p;
            // Try to make do with what we have.  That can't
            // hurt.  We do not try smaller requests, since that tends
            // to result in disaster on multi-process machines.
                //这部分不理解，为什么只能从大的block中分配呢？
            for (__i = __size; __i <= _MAX_BYTES; __i += _ALIGN) {
                __my_free_list = _S_free_list + _S_freelist_index(__i);
                __p = *__my_free_list;
                if (0 != __p) {
                          //在freeList 中，我们找到了一个大的block，并且里面有数据
                    *__my_free_list = __p -> _M_free_list_link;
                    _S_start_free = (char*)__p;
                    _S_end_free = _S_start_free + __i;
                          //从大的freelist中，我们分配出一个来到内存池，然后递归。这次没有
                              //意外，会找到足够的内存
                    return(_S_chunk_alloc(__size, __nobjs));
                    // Any leftover piece will eventually make it to the
                    // right free list.
                }
            }
                //还是没有满足要求，调用一级分配器看oom机制，是否能够帮助我们
     _S_end_free = 0; // In case of exception.
            _S_start_free = (char*)malloc_alloc::allocate(__bytes_to_get);
            // This should either throw an
            // exception or remedy the situation.  Thus we assume it
            // succeeded.
        }
          //扩充了内存池大小
        _S_heap_size += __bytes_to_get;
        _S_end_free = _S_start_free + __bytes_to_get;
        return(_S_chunk_alloc(__size, __nobjs));//根据新的内存池大小，修正__nobjs
    }//end else
     //这里我们看出了，为什么是8的倍数，所以，我们分配的大的block，肯定会在小的block中找到位置，而不会
      //浪费掉当然，具体的理由肯定还有更多，需要去了解更多的内存方面的知识才能理解。
}

内存管理这里仅仅是一个最最基本的梳理，事实上其实仅仅是照本宣科而已，因为这里面有太多的细节需要去琢磨。STL设计这样的原因是什么？他的分配回收机制为什么是这样？他的分配粒度，以及处理分配不足的手段。对我来说都是未知，不过好在目前的确不需要思考过多这些问题。仅仅是上层的封装和简单功能的实现就已经让我受益匪浅了。这些问题还是留给时间去沉淀这些未知吧。

heap，大家都非常了解。大学学的时候必须会的内容，要不考试很难过关。只是当时并没有学习明白。只是被老师和考试强了。完全是机械的记忆。觉得真是太对不起自己这个专业了。最近再看STL，也就有了这一篇老生重弹。

在很多情况下，我们非常关心一个集合中的最大元素。并希望能够从集合中最快速度找到并删除。为了整体的效率，我们需要在这个集合中插入元素，查找最大元素，删除最大元素能够综合最快。使用binary heap便是一种不错的选择之一。而且能够在O(logN)插入，删除元素，查找最大元素在常数时间下。

　　Binary heap 是一种complete binary tree（完全二叉树）。所以我们可以放心的使用简单的数组来保存数据而不需要担心浪费空间。维持树的父子关系也简单快速,而且整个过程都在原地进行。

　　Heap 可以按照排列顺序分为大顶堆，小顶堆。 这里讨论的堆默认为大顶堆。每个节点的值大于等于其子节点的值。

一个典型的大顶堆。

了解heap，让我们从最简单的插入开始。

push_heap 　　在插入之前，首先确定的是，我们已经构成了一个完整的堆，为了保证完全二叉树的要求，我们只能在数组最后一个元素位置后增加元素。这个新家伙，显然有可能破坏了我们整个堆的结构。那么我们需要给这个新来的找到他的位置。

　　总结这个过程。其实就是在整个树中增加一个叶子节点，然后，一直到比较到跟或是比父节点小为止。可以看出，整个这次比较最大次数为树的深度，O(logN)。

template <class _RandomAccessIterator>
inline void
push_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
  __push_heap_aux(__first, __last,
                  __DISTANCE_TYPE(__first), __VALUE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
inline void
__push_heap_aux(_RandomAccessIterator __first,
                _RandomAccessIterator __last, _Distance*, _Tp*)
{
  __push_heap(__first, _Distance((__last - __first) - 1), _Distance(0), 
              _Tp(*(__last - 1)));
    //这里将最后一个元素设定为holeIndex。也就是说，这时新数据已经在底部的数组中了。
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__push_heap(_RandomAccessIterator __first,
            _Distance __holeIndex, _Distance __topIndex, _Tp __value)
{
  _Distance __parent = (__holeIndex - 1) / 2;
   //不断移动holeIndex，直到大于等于父节点或到达根。
  while (__holeIndex > __topIndex && *(__first + __parent) < __value) {
    *(__first + __holeIndex) = *(__first + __parent);
    __holeIndex = __parent;
    __parent = (__holeIndex - 1) / 2;
  }    
  *(__first + __holeIndex) = __value;
}

Pop_heap 　　Pop_heap用来将最大值从堆中取走，当将顶部元素移动走之后，在根部就产生了一个hole。我们需要找到合适的数据将这个hole添上，而且我们还要尽可能的保存堆的性质（大小关系，和完全二叉树），所以，我们将顶部元素和最后一个元素交换。并将堆的大小减一。那么我们的新的根元素，显然违反了堆中大小关系的约定。所以，我们需要重新调整堆。而且，我们更爽的是，这个错误的堆的左右二个子树分别满足堆的性质，那么我需要找到hole节点的2个子节点中最大的和我们的hole 比较，并沿着大的子节点方向，直到叶子或是我们的这个hole满足大小关系。

template <class _RandomAccessIterator>
inline void pop_heap(_RandomAccessIterator __first, 
                     _RandomAccessIterator __last)
{
  __pop_heap_aux(__first, __last, __VALUE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp>
inline void
__pop_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last,
               _Tp*)
{
  __pop_heap(__first, __last - 1, __last - 1, 
             _Tp(*(__last - 1)), __DISTANCE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp, class _Distance>
inline void
__pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last,
           _RandomAccessIterator __result, _Tp __value, _Distance*)
{
  *__result = *__first;
   //这里将之前堆中最后一个元素的值保存在__value，并将根元素的值移动到最后一个元素
  //然后将--last，也就是说，我们这里构造了一个更小的堆，并且只是根元素有问题。
  //那么我们剩下的就是调整这个小堆。
  __adjust_heap(__first, _Distance(0), _Distance(__last - __first), __value);
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__adjust_heap(_RandomAccessIterator __first, _Distance __holeIndex,
              _Distance __len, _Tp __value)
{
  _Distance __topIndex = __holeIndex;
  _Distance __secondChild = 2 * __holeIndex + 2; //找到hole节点的右子节点
  while (__secondChild < __len) {
    if (*(__first + __secondChild) < *(__first + (__secondChild - 1)))
      __secondChild--;// __secondChild指向最大的子节点。
    *(__first + __holeIndex) = *(__first + __secondChild);
    //这里SGI STL并没有和我们的__value比较大小，所以，我们这里得到的holeIndex可能是错误的。或者说只是一
    //个大概的位置。（很多优化的算法，并不是一次性完成的，而是去分情况或是其他什么的多种复合）。
    //这里可能是SGI STL在这里优化，侯捷大师，似乎在这里打个一个盹。
    __holeIndex = __secondChild;
    __secondChild = 2 * (__secondChild + 1);
  }
  if (__secondChild == __len) {//当我们的根节点没有右节点时，就搞他左边的兄弟。
    *(__first + __holeIndex) = *(__first + (__secondChild - 1));
    __holeIndex = __secondChild - 1;
  }
  //侯捷大师注 ："将与调整值添入目前洞号内，注意，此时肯定满足次序特性"
  //“依侯捷之见，下面直接改为 *(__first + __holeIndex) = value;应该可以”
  //我这里认为侯捷大师在这里打盹了，这句话如果改了的话，整个过程就出错了。
  //之前的优化，可以减少一些不必要的比较次数。但是如果把这个也省了。结果不能保证正确。
  //我们的结果不一定满足次序特性。
  __push_heap(__first, __holeIndex, __topIndex, __value);
}

比如如下例子。

当push_heap的时候，如果直接*(first + holeIndex) = VALUE,那么就会成为这个样子。

　　所以，必须要再一次经过__push_heap，再一次修正 24->16->65这条路径。保证真正的顺序。

而SGI这样实现是为了减少一些不必要的比较。

Sort_heap 　　在搞定这些基本操作之后，我们发现，我们只需要执行一次次的pop_heap，我们就可以把数据按照一定的顺序跑列出来。而这也就是堆排序。

template <class _RandomAccessIterator>

void sort_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)

{

while (__last - __first > 1)

pop_heap(__first, __last--);

}

　　我们发现，每一次pop_heap操作是O(logN)。整个数列排序结果是O(n*logN)。这已经达到比较方法的极限。而且是原地排序，而且最坏情况依然不变。heap sort的确是一个非常出色的算法。

哦，扯了这么多，我们heap的好处不少，可是如何构造heap呢？

Make_heap 　　还记得adjust_heap， 这个函数，可以在左右子树满足条件情况下调整树，那么我们完全可以从下到上逐渐构造成一个符合我们要求的树。而且，树的叶子节点是没有孩子的。所以，我们可以更快的只是从中间开始。 初略的估算下，每一次adjust_heap，O(logN)，一半的节点，O(n*logN)，但其实我们可以做的更快。 建堆的复杂度可以达到O(n)的线性。

template <class _RandomAccessIterator>
inline void
make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
  __make_heap(__first, __last,
              __VALUE_TYPE(__first), __DISTANCE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp, class _Distance>
void
__make_heap(_RandomAccessIterator __first,
            _RandomAccessIterator __last, _Tp*, _Distance*)
{
  if (__last - __first < 2) return;//当长度小于等于1时，我们就不需要排序了。
  _Distance __len = __last - __first;
  _Distance __parent = (__len - 2)/2;//找到第一个非叶子节点。

  while (true) {
    __adjust_heap(__first, __parent, __len, _Tp(*(__first + __parent)));
    if (__parent == 0) return;
    __parent--;
  }
}

sequence containers

Array
Vector
Heap
Priority_queue
List
sList（not in standard）
Deque
Stack
Queue

Sequence Containers 其中的元素 都是可序的（ordered），但并不一定有序（sorted）。STL 中有vector ，list ，deque，stack，queue，priority_queue等序列容器。Stack queue 由于只是将deque重新封装而成，在技术上被归类为一种配接器(adapter)。

Vector Vector 的数据为动态空间，随着元素的加入。内部会通过机制自行扩充空间，以容纳新元素。 Vector 的效率，在于对大小的控制，重新分配时数据移动效率。当空间不足时，vector会选择策略扩充容量。 Vector resize之后，很可能使所有迭代器均失效。 插入后，插入点之前的Iterator 有效，其他则无效。eraser迭代器失效。 Vector实现 Vector 实现比较简单。这里仅仅作为打开SGI STL的敲门砖。

我这里的SGI STL 对vector有进行了进一步封装。在头文件中，也给出了我们的解释。

// The vector base class serves two purposes. First, its constructor

// and destructor allocate (but don’t initialize) storage. This makes

// exception safety easier. Second, the base class encapsulates all of

// the differences between SGI-style allocators and standard-conforming

// allocators.

这里根据 宏 STL_USE_STD_ALLOCATORS 来决定是否资源分配器。如果定义了STL_USE_STD_ALLOCATORS， 则使用allocator< _Tp >，否则为alloc

//这里的 _Vector_base 为我们隐藏了 使用STL 标准分配器，和SGI 自己特有的分配器之间的不同
//我们现在先把这里具体的分配细节透明。
//这是，使用SGI 自己的分配器
template <class _Tp, class _Alloc> 
class _Vector_base {
public:
  typedef _Alloc allocator_type;
  allocator_type get_allocator() const { return allocator_type(); }

  _Vector_base(const _Alloc&)
    : _M_start(0), _M_finish(0), _M_end_of_storage(0) {}
  _Vector_base(size_t __n, const _Alloc&)
    : _M_start(0), _M_finish(0), _M_end_of_storage(0) 
  {
    _M_start = _M_allocate(__n);
    _M_finish = _M_start;
    _M_end_of_storage = _M_start + __n;
  }

  ~_Vector_base() { _M_deallocate(_M_start, _M_end_of_storage - _M_start); }

protected:
  _Tp* _M_start;
  _Tp* _M_finish;
  _Tp* _M_end_of_storage;

  typedef simple_alloc<_Tp, _Alloc> _M_data_allocator;
  _Tp* _M_allocate(size_t __n)
    { return _M_data_allocator::allocate(__n); }
  void _M_deallocate(_Tp* __p, size_t __n) 
    { _M_data_allocator::deallocate(__p, __n); }
};


template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) >
class vector : protected _Vector_base<_Tp, _Alloc> 
{
private:
  typedef _Vector_base<_Tp, _Alloc> _Base;
public:
  typedef _Tp value_type;
  typedef value_type* pointer;
  typedef const value_type* const_pointer;
  typedef value_type* iterator;
  typedef const value_type* const_iterator;
  typedef value_type& reference;
  typedef const value_type& const_reference;
  typedef size_t size_type;
  typedef ptrdiff_t difference_type;

  typedef typename _Base::allocator_type allocator_type;
  allocator_type get_allocator() const { return _Base::get_allocator(); }
…
...
};

分析vector，首先看他的Iterator。

typedef value_type* iterator;

typedef const value_type* const_iterator;

我们可以看出，vector的Iterator 就是一个指针。若是定义

vector:: iterator iter1;

vector:: iterator iter2;

那么，Iter1 其实，就是int *， iter2其实就是RECT * 。

看一下，部分的vector 函数，也是我们常常使用的。

Vector 的数据，什么时候被释放。我们需要看析构函数。

~vector() { destroy(_M_start, _M_finish); }

template <class _ForwardIterator>
inline void destroy(_ForwardIterator __first, _ForwardIterator __last) {
  __destroy(__first, __last, __VALUE_TYPE(__first));
}

#define __VALUE_TYPE(__i)        __value_type(__i)

下面是2个偏特化版本。可以看出，在一些特殊情况下，我们找到了最快速的方法。什么也不干。

inline void destroy(char*, char*) {}
inline void destroy(wchar_t*, wchar_t*) {}

template <class _Iter>
inline typename iterator_traits<_Iter>::value_type*
__value_type(const _Iter&)
{
   //这里，仅仅构造一个临时对象（准确说是指针）来做返回值，事实上，我们不关心他到底是个什么，只是关心她的类型。
    //用这个类型来激发函数重载，所以，用0来构造也无妨。
  return static_cast<typename iterator_traits<_Iter>::value_type*>(0);
}

template <class _ForwardIterator, class _Tp>
inline void
__destroy(_ForwardIterator __first, _ForwardIterator __last, _Tp*)//这里多了一个接受这个类型对象参数
{
    //根据这个类型_Tp，我们根据__type_traits<_Tp>，找到了这个类型是否有has_trivial_destructor。
  typedef typename __type_traits<_Tp>::has_trivial_destructor _Trivial_destructor;
    //然后构造一个临时的对象来激发函数重载。
  __destroy_aux(__first, __last, _Trivial_destructor());
}

//下面2个便是特化后的结果。
//__false_type,我们老老实实的该干什么干什么。
template <class _ForwardIterator>
inline void
__destroy_aux(_ForwardIterator __first, _ForwardIterator __last, __false_type)
{
  for ( ; __first != __last; ++__first)
    destroy(&*__first);
}

//__true_type 我们实在是没有这个必要和他纠结了。
template <class _ForwardIterator>
inline void __destroy_aux(_ForwardIterator, _ForwardIterator, __true_type) {}

这是可能怀疑，内存到那里释放呢？ 别忘了，我们的vector 是继承自_Vector_base，内存释放，管理都隐藏在他那里。

~Vector_base() { M_deallocate(M_start, M_end_of_storage - _M_start); }

这里才真正的执行内存的回收。但是这里又涉及到了SGI STL 的内存管理，这部分是给操作系统，还是给内存池呢？

在没有研究过细致的内存管理之前。我们还是将这里透明吧。

基本操作

iterator begin() { return _M_start; }
const_iterator begin() const { return _M_start; }
iterator end() { return _M_finish; }
const_iterator end() const { return _M_finish; }
size_type size() const { return size_type(end() - begin()); }
size_type capacity() const { return size_type(_M_end_of_storage - begin()); }
bool empty() const { return begin() == end(); }

void push_back(const _Tp& __x) {
    if (_M_finish != _M_end_of_storage) {
      construct(_M_finish, __x);
      ++_M_finish;
    }
    else
      _M_insert_aux(end(), __x);
  }

  void push_back() {
    if (_M_finish != _M_end_of_storage) {
      construct(_M_finish);
      ++_M_finish;
    }
    else
      _M_insert_aux(end());
  }

void resize(size_type __new_size, const _Tp& __x) {
    if (__new_size < size()) 
      erase(begin() + __new_size, end());
    else
      insert(end(), __new_size - size(), __x);
  }

  void resize(size_type __new_size) { resize(__new_size, _Tp()); }

删除 erase

iterator erase(iterator __position) {
    if (__position + 1 != end())
      copy(__position + 1, _M_finish, __position);
    --_M_finish;
    destroy(_M_finish);
    return __position;
  }
  iterator erase(iterator __first, iterator __last) {
    iterator __i = copy(__last, _M_finish, __first);
    destroy(__i, _M_finish);
    _M_finish = _M_finish - (__last - __first);
    return __first;
  }

Copy 是全局函数，操作简单，同样有多个特化版本。Vector 和一般数组的删除动作一样，将后面元素一个个往前搬。最后修改个数。

插入 insert

iterator insert(iterator __position, const _Tp& __x) {
    size_type __n = __position - begin();
    if (_M_finish != _M_end_of_storage && __position == end()) {
      construct(_M_finish, __x);
      ++_M_finish;
    }
    else
      _M_insert_aux(__position, __x);
    return begin() + __n;
  }
  iterator insert(iterator __position) {
    size_type __n = __position - begin();
    if (_M_finish != _M_end_of_storage && __position == end()) {
      construct(_M_finish);
      ++_M_finish;
    }
    else
      _M_insert_aux(__position);
    return begin() + __n;
  }


template <class _Tp, class _Alloc>
void
vector<_Tp, _Alloc>::_M_insert_aux(iterator __position)
{
  if (_M_finish != _M_end_of_storage) {
    construct(_M_finish, *(_M_finish - 1));
    ++_M_finish;
    copy_backward(__position, _M_finish - 2, _M_finish - 1);
    *__position = _Tp();
  }
  else {
    const size_type __old_size = size();
    const size_type __len = __old_size != 0 ? 2 * __old_size : 1;
    iterator __new_start = _M_allocate(__len);
    iterator __new_finish = __new_start;
    __STL_TRY {
      __new_finish = uninitialized_copy(_M_start, __position, __new_start);
      construct(__new_finish);
      ++__new_finish;
      __new_finish = uninitialized_copy(__position, _M_finish, __new_finish);
    }
    __STL_UNWIND((destroy(__new_start,__new_finish), 
                  _M_deallocate(__new_start,__len)));
    destroy(begin(), end());
    _M_deallocate(_M_start, _M_end_of_storage - _M_start);
    _M_start = __new_start;
    _M_finish = __new_finish;
    _M_end_of_storage = __new_start + __len;
  }
}

的确很简单，和我们在学校学的并没有什么大的不同，只是在对新增元素的构造上不同。

construct(__new_finish)，

construct(_M_finish, *(_M_finish - 1));

以上construct是全局函数，同样有特化版本。将类的构造分成，资源分配 + 构造函数，来做到提高效率。这样在大量数据上效果应该很明显，并没有具体测试。

对一次插入大量元素时，vector 的策略是。
if (插入元素个数 == 0 ) return
if (判断容量是否足够)
{
    if (插入点后的元素个数 > 待插入元素个数)
    {
       按照最后一个元素，构造插入元素个数个元素。
         向插入点数据向后搬运。
         移动指针。
         将待插入元素顺次插入。
    }
    else
    {
       先以__x构造元素，在不需要移动位置的地方。
         将原来的元素，移动到最后。
         在插入位置处，以__x构造元素。
    }
}
else
{
    根据策略分配空间（这里至少PJ 和SGI的策略不同，这里应该和不同的内存管理策略有关）
    将插入点之前的原有的数据复制到新空间
    依次复制新元素到新空间。
    依次复制原来数据到新空间
}


template <class _Tp, class _Alloc>
void vector<_Tp, _Alloc>::insert(iterator __position, size_type __n, const _Tp& __x)
{
  if (__n != 0) {
    if (size_type(_M_end_of_storage - _M_finish) >= __n) {
      _Tp __x_copy = __x;
      const size_type __elems_after = _M_finish - __position;
      iterator __old_finish = _M_finish;
      if (__elems_after > __n) {
        uninitialized_copy(_M_finish - __n, _M_finish, _M_finish);
        _M_finish += __n;
        copy_backward(__position, __old_finish - __n, __old_finish);
        fill(__position, __position + __n, __x_copy);
      }
      else {
        uninitialized_fill_n(_M_finish, __n - __elems_after, __x_copy);
        _M_finish += __n - __elems_after;
        uninitialized_copy(__position, __old_finish, _M_finish);
        _M_finish += __elems_after;
        fill(__position, __old_finish, __x_copy);
      }
    }
    else {
      const size_type __old_size = size();        
      const size_type __len = __old_size + max(__old_size, __n);
      iterator __new_start = _M_allocate(__len);
      iterator __new_finish = __new_start;
      __STL_TRY {
        __new_finish = uninitialized_copy(_M_start, __position, __new_start);
        __new_finish = uninitialized_fill_n(__new_finish, __n, __x);
        __new_finish
          = uninitialized_copy(__position, _M_finish, __new_finish);
      }
      __STL_UNWIND((destroy(__new_start,__new_finish), 
                    _M_deallocate(__new_start,__len)));
      destroy(_M_start, _M_finish);
      _M_deallocate(_M_start, _M_end_of_storage - _M_start);
      _M_start = __new_start;
      _M_finish = __new_finish;
      _M_end_of_storage = __new_start + __len;
    }
  }
}