Introduction

机器学习很久之前就已经热得不行了，直到最近这几个星期，自己才打算了解一些这方面的东西。原因大概有这么3点。

1. 自从Andrew Ng 加入我厂之后(虽然和我毛关系也没有)，总觉得还是需要围观一下这个令他兴奋的领域。
2. 在听了IDL的有关手环算法分享后(其实毛也没有听懂), 在知道了一大堆的名词如最小二乘、梯度下降、SVM。以及里面很多的线性代数，微积分的概念，让我觉得这是一个很好的回收自己大学时期的沉默成本(微积分、现代是我在学校里面不多的用心学过的课程)的好机会。总之就是对这些很感兴趣。
3. 前一段时间受组里高工分享睡眠算法影响，对这种阅读paper，然后优化算法的过程感到很开心。

有了这3条，足够我忙活好几个月了 : )

Background

在机器学习中，有2个很大的思路监督学习(supervised learning)和非监督学习(unsupervised learning)

监督学习，用通俗的话来说就是你知道问题的答案，需要计算机给出一个更标准的答案。

非监督学习，用通俗的话来说就是物以类聚，人以群分。我们拿到了很多数据，但是不知道问题的答案，希望计算机给我们提供思路。

在生产环境中，往往采用混合模式。比如图片搜索，如何能够查找网页中判断那个图片是老虎，那个是狗。就有2个思路。

1. 根据图片周围的文字。
2. 图片的图像数据分析。

2个角度相互校验，稳定之后，就可以产生足够的标注信息了。

线性回归(Linear regression)

线性回归主要用于手环的里程部分的计算，涉及到更细节的是 最小二乘，梯度下降。这里从先从最简单的一元线性回归开始。

一元线性回归(Linear regression with one variable)

Regression Problem : Predict real-valued output

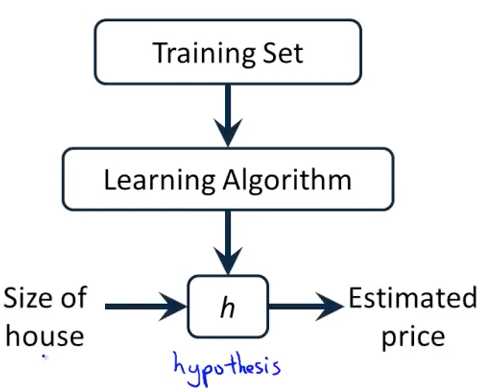1-1 算法运行的过程

最关键的在于如何描述hypothesis。

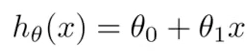1-2 一元线性回归中的hypothesis函数

那么应该如何选取参数呢？直觉告诉我们这个直线需要尽可能的拟合我们的数据集。

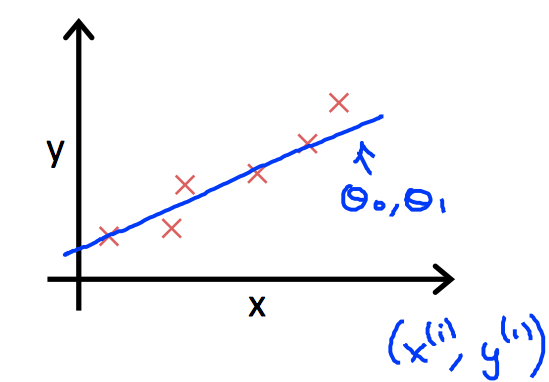1-3 线性回归的目标函数

通过下面的cost function 来评估参数的好坏。算法的目标也很清晰，让函数越小越好。

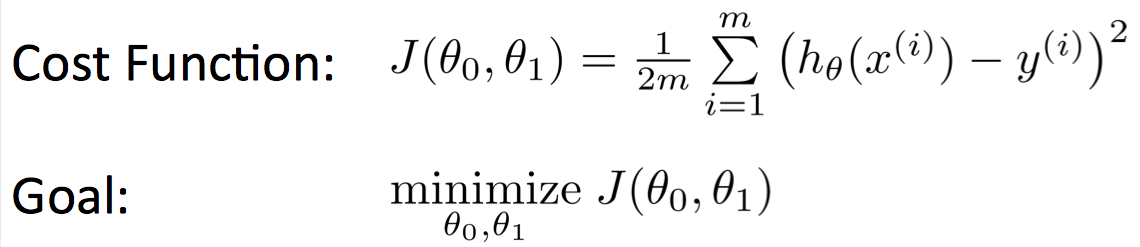1-4 cost function

那个这个cost function 到底是个什么样子呢？

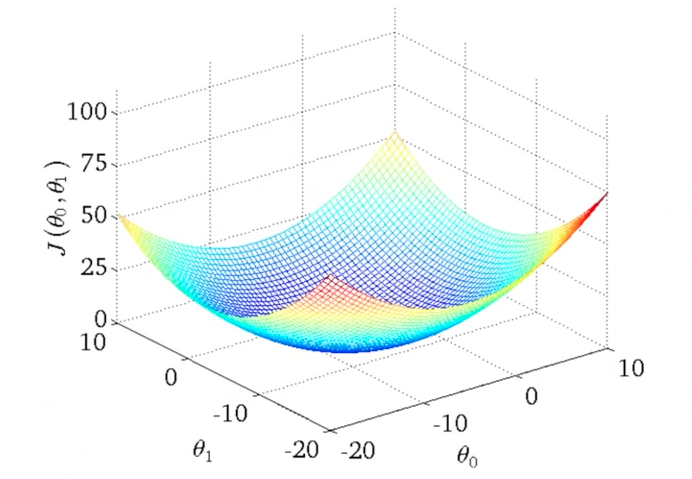1-5 图形化的cost function

当然这个图还是看起来比较麻烦，Andrew 用了更为简单绘制的图来表示（有点类似等高线）。 相同的圆圈上，有着相同的cost function value。这里可以看到和上面的图一样，有一个极值。

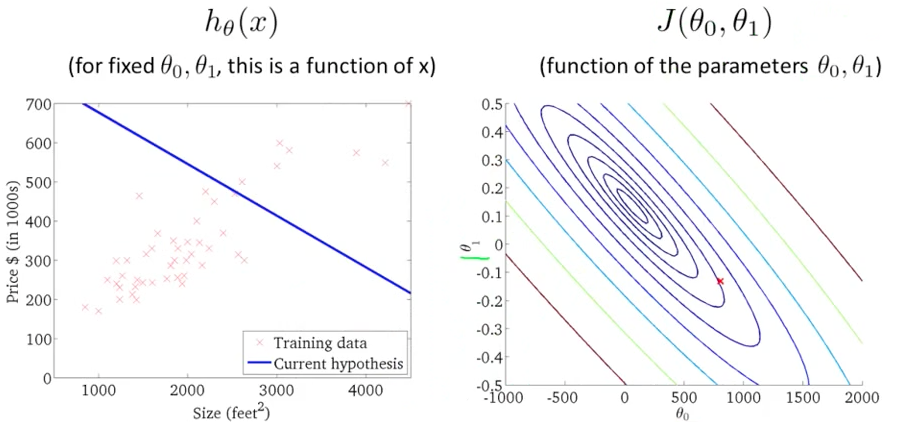1-6 一个比较差的选择

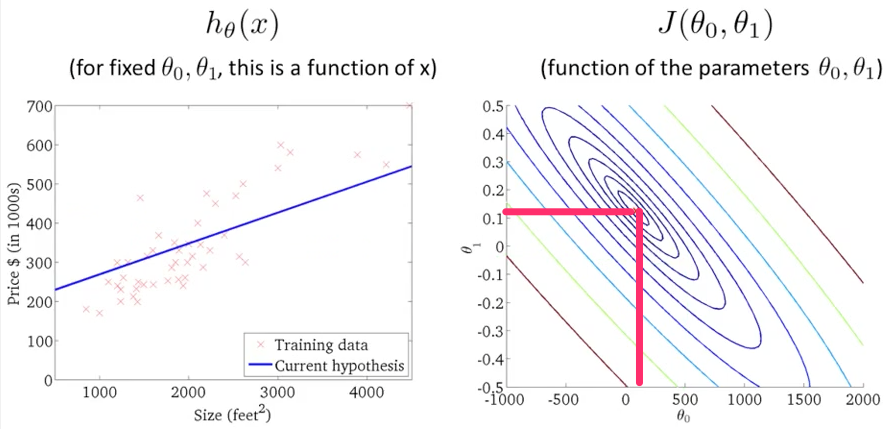1-7 一个很接近极值的选择

梯度下降 (Gradient descent)

梯度下降，不仅仅是用于线性回归，也可以用在其他机器学习的场景下。

1-8 梯度下降的思路（2个参数的情况）

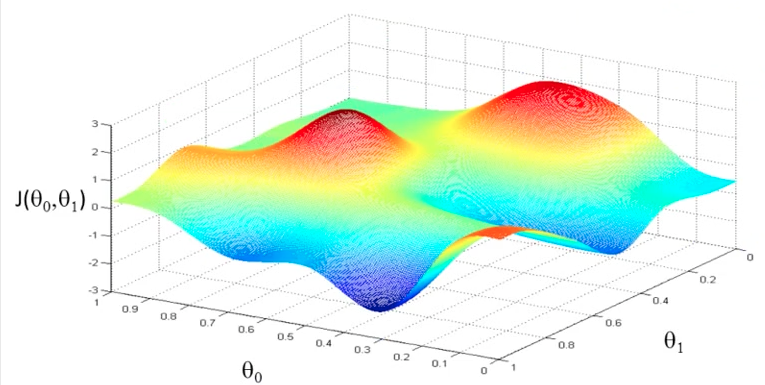1-9 梯度下降函数图形（2个参数的情况）

我们的目标是寻找这个图形中的最小值，也就是靠近蓝色的地方。直觉告诉我们，我们先随机一个点，然后沿着最大的坡度向下走最后就可以走到一个极值里。

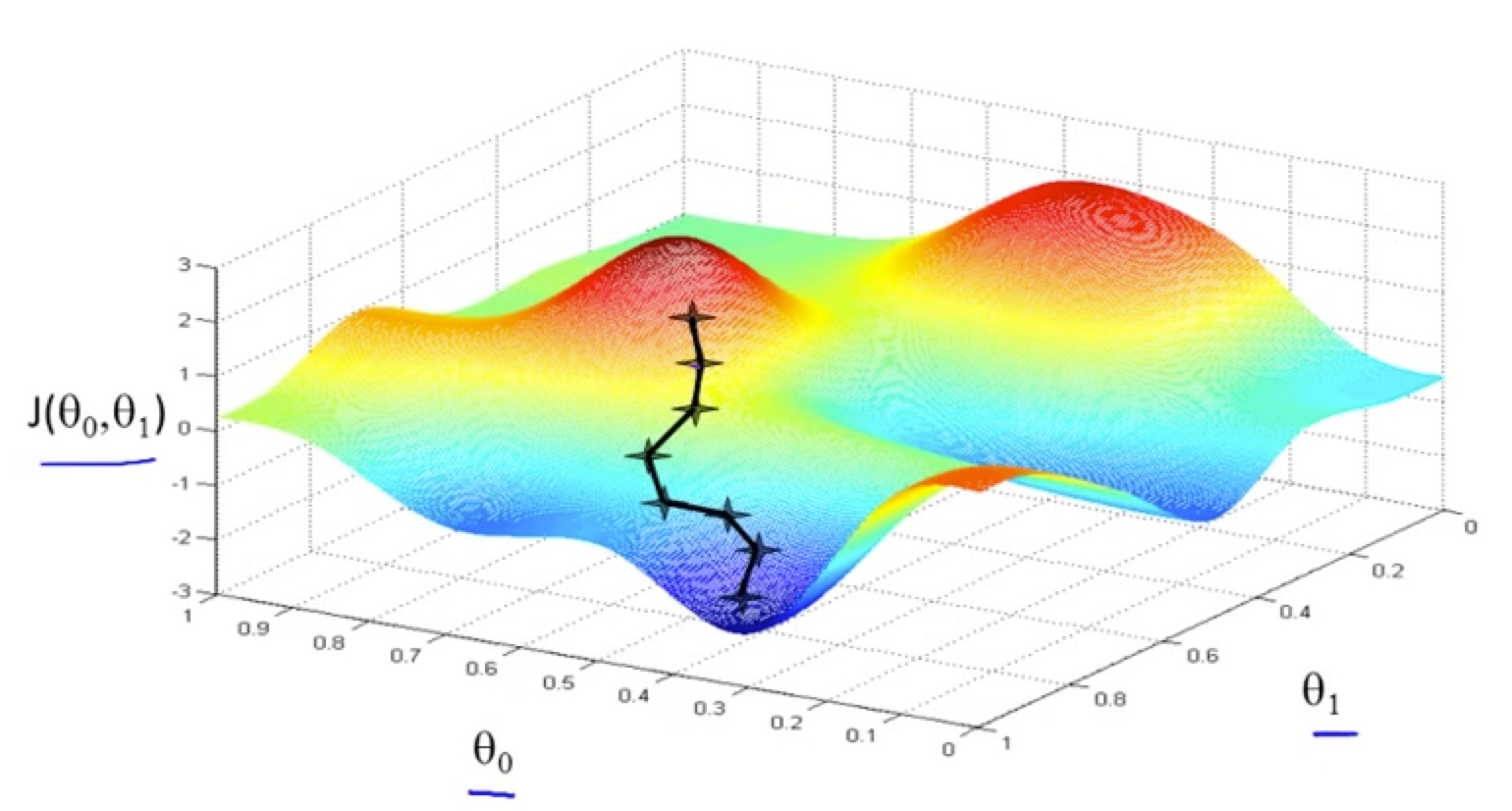1-10 一条算法路径，全局最优

这个算法也有问题，随着第一个点的位置不同，我们可能找到一个局部最优的解，而不是全局最优。

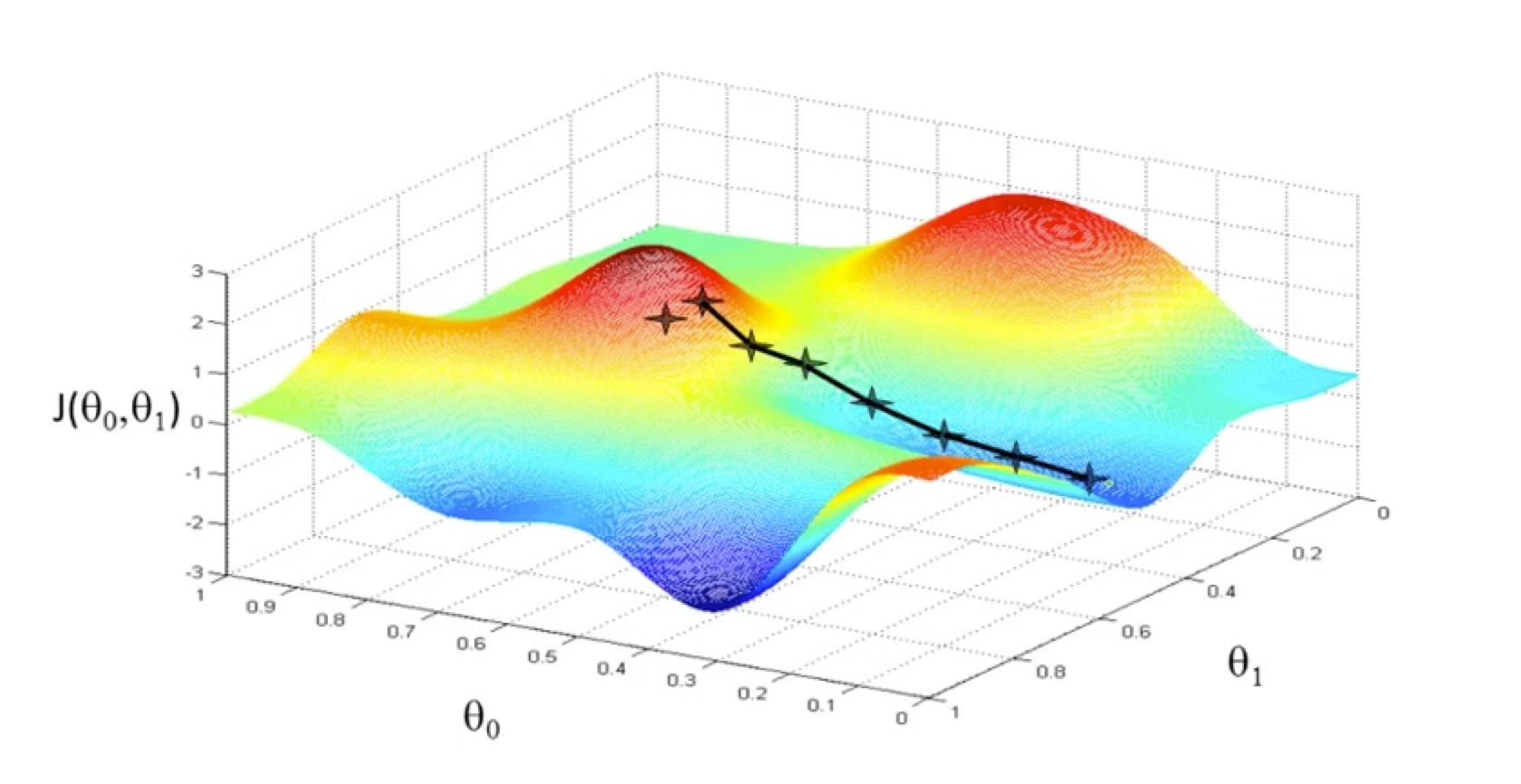1-11 另一条算法路径，局部最优

好在在很多实际问题中，我们遇到的情况要好很多，往往只有一个极值。

那么梯度下降的算法就可以简单的描述出来，分别计算2个维度的偏导数，直到函数收敛

1-12

通过分别计算偏导数,a 为learning rate，决定每一步的步长，太小函数收敛很慢，太大则可能无法找到极值，甚至函数无法收敛。

这里Andrew 着重指出了一个叫做同步更新的概念

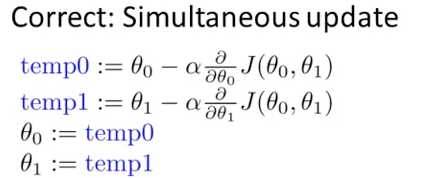1-13

如果不同步更新，最后也可以得到极致，但是Andrew 更推荐计算完成所有的参数之后，再一起同步更新。

梯度下降和一元线性回归

将图1-4分别偏导后

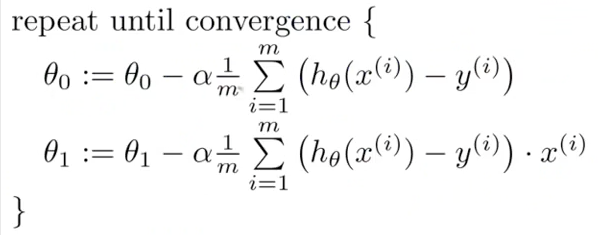1-14 算法公式

其他

1. 根据上面的算法，如果我们的cost function 在一些地方不可导，那算法不就没法继续了？
2. 有其他的方法，可以不去循环计算而是直接根据工具计算

梯度下降和一般化的线性回归

很多时候我们不仅仅满足2个参数，决定事情的因素很多，我们需要更一般化的公式。

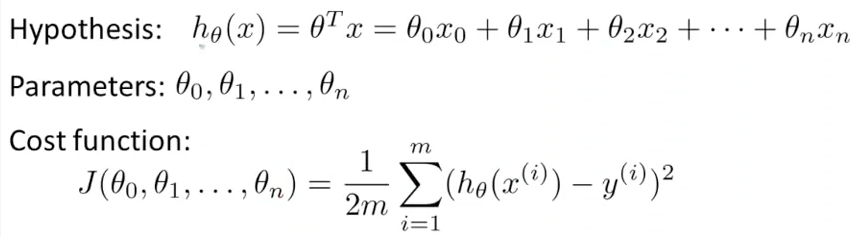1-15

算法

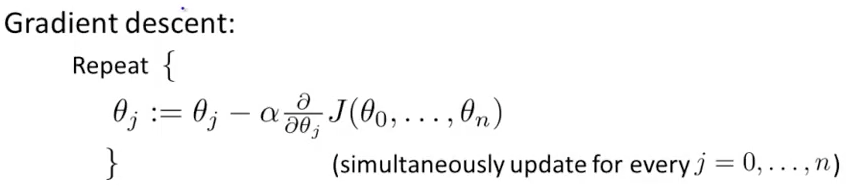1-16

分别求偏导后

1-17

梯度下降生产环境中的一些技巧

Feature Scaling

思路: 希望所有的feature在相同或是类似的范围之内，这样梯度下降会更快收敛。

下图是feature的范围不在一起的运算过程，可以看出来不是圆形，2个维度调整的步长不一样，导致很多反复

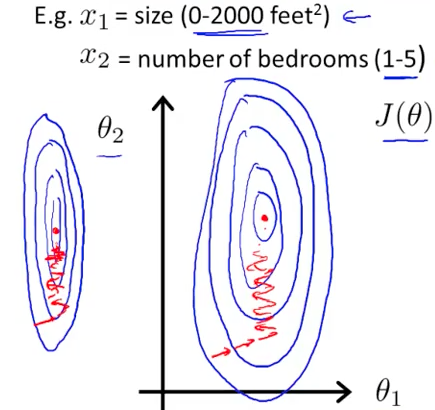1-18 红色箭头表示算法的一次迭代

下图则是调整过的feature，好了很多

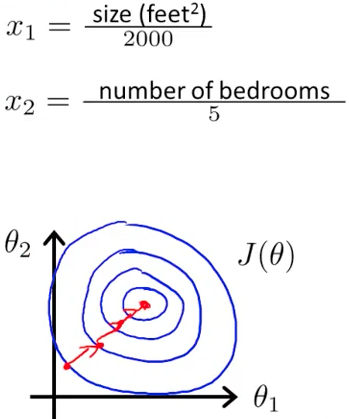1-19 红色箭头表示算法的一次迭代

更一般的，Andrew 推荐每一个feature放在[-1, 1]区间范围内

Learning Rate

说到Learning Rate 就不能不提收敛(convergence)。一般应该定义多大的阀值来判断是否收敛呢？

1-20 Andrew 并不推荐使用一个阀值来判断是否收敛

Andrew 更推荐用图表的形式，因为这个不仅仅可以看到是否马上收敛，而且还能看到算法是否运行正常，是不是一些参数的问题，导致算法无法收敛。

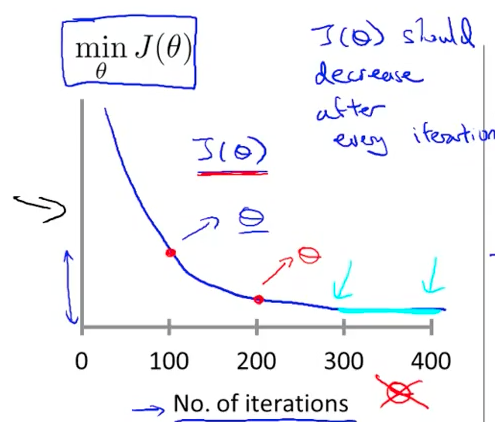1-21

下图是2个出了问题的J函数，通常来说是Learning Rate 过大。

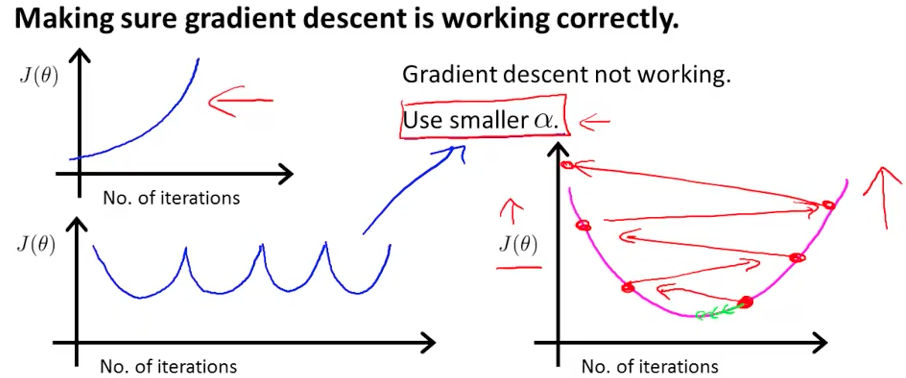1-22 一些过大的Learning Rate 导致的图形

最后Andrew 还提供了一些practice的Learning Rate 选取方法，比如一些0.001, 0.003, 0.01, 0.03, 0.1, …

参考

Coursera 《Machine Learning》 Stanford Andrew Ng