SGI STL 学习笔记三 heap

heap，大家都非常了解。大学学的时候必须会的内容，要不考试很难过关。只是当时并没有学习明白。只是被老师和考试强了。完全是机械的记忆。觉得真是太对不起自己这个专业了。最近再看STL，也就有了这一篇老生重弹。

在很多情况下，我们非常关心一个集合中的最大元素。并希望能够从集合中最快速度找到并删除。为了整体的效率，我们需要在这个集合中插入元素，查找最大元素，删除最大元素能够综合最快。使用binary heap便是一种不错的选择之一。而且能够在O(logN)插入，删除元素，查找最大元素在常数时间下。

　　Binary heap 是一种complete binary tree（完全二叉树）。所以我们可以放心的使用简单的数组来保存数据而不需要担心浪费空间。维持树的父子关系也简单快速,而且整个过程都在原地进行。

　　Heap 可以按照排列顺序分为大顶堆，小顶堆。这里讨论的堆默认为大顶堆。每个节点的值大于等于其子节点的值。

一个典型的大顶堆。

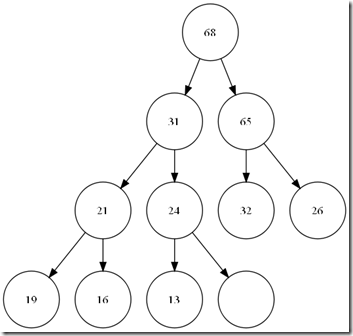
alt text

了解heap，让我们从最简单的插入开始。

push_heap 　　在插入之前，首先确定的是，我们已经构成了一个完整的堆，为了保证完全二叉树的要求，我们只能在数组最后一个元素位置后增加元素。这个新家伙，显然有可能破坏了我们整个堆的结构。那么我们需要给这个新来的找到他的位置。

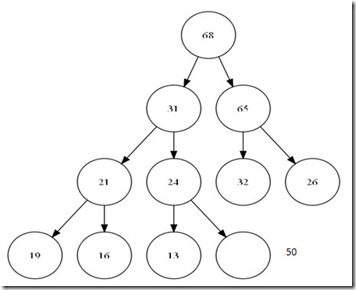
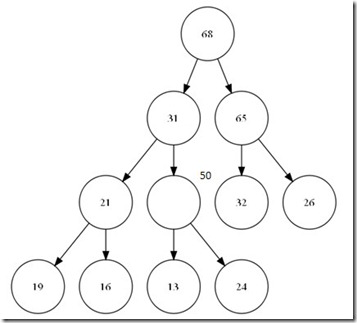
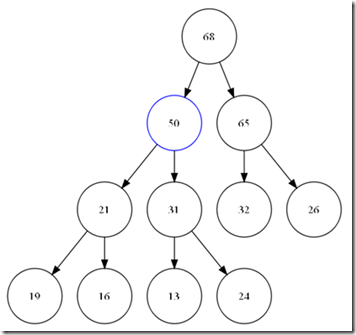
alt text

　　总结这个过程。其实就是在整个树中增加一个叶子节点，然后，一直到比较到跟或是比父节点小为止。可以看出，整个这次比较最大次数为树的深度，O(logN)。

template <class _RandomAccessIterator>
inline void
push_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
  __push_heap_aux(__first, __last,
                  __DISTANCE_TYPE(__first), __VALUE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
inline void
__push_heap_aux(_RandomAccessIterator __first,
                _RandomAccessIterator __last, _Distance*, _Tp*)
{
  __push_heap(__first, _Distance((__last - __first) - 1), _Distance(0), 
              _Tp(*(__last - 1)));
    //这里将最后一个元素设定为holeIndex。也就是说，这时新数据已经在底部的数组中了。
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__push_heap(_RandomAccessIterator __first,
            _Distance __holeIndex, _Distance __topIndex, _Tp __value)
{
  _Distance __parent = (__holeIndex - 1) / 2;
   //不断移动holeIndex，直到大于等于父节点或到达根。
  while (__holeIndex > __topIndex && *(__first + __parent) < __value) {
    *(__first + __holeIndex) = *(__first + __parent);
    __holeIndex = __parent;
    __parent = (__holeIndex - 1) / 2;
  }    
  *(__first + __holeIndex) = __value;
}

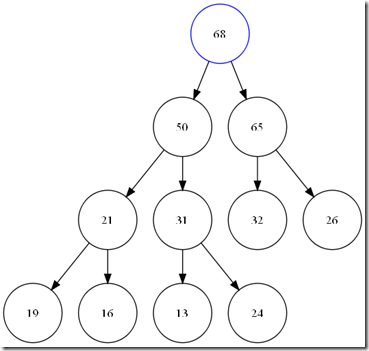
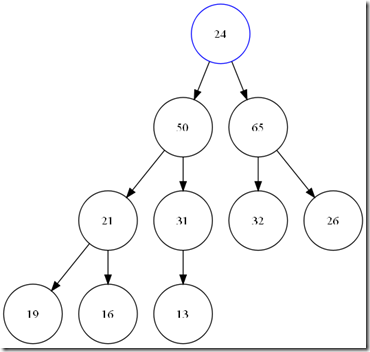
Pop_heap 　　Pop_heap用来将最大值从堆中取走，当将顶部元素移动走之后，在根部就产生了一个hole。我们需要找到合适的数据将这个hole添上，而且我们还要尽可能的保存堆的性质（大小关系，和完全二叉树），所以，我们将顶部元素和最后一个元素交换。并将堆的大小减一。那么我们的新的根元素，显然违反了堆中大小关系的约定。所以，我们需要重新调整堆。而且，我们更爽的是，这个错误的堆的左右二个子树分别满足堆的性质，那么我需要找到hole节点的2个子节点中最大的和我们的hole 比较，并沿着大的子节点方向，直到叶子或是我们的这个hole满足大小关系。

alt text

template <class _RandomAccessIterator>
inline void pop_heap(_RandomAccessIterator __first, 
                     _RandomAccessIterator __last)
{
  __pop_heap_aux(__first, __last, __VALUE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp>
inline void
__pop_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last,
               _Tp*)
{
  __pop_heap(__first, __last - 1, __last - 1, 
             _Tp(*(__last - 1)), __DISTANCE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp, class _Distance>
inline void
__pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last,
           _RandomAccessIterator __result, _Tp __value, _Distance*)
{
  *__result = *__first;
   //这里将之前堆中最后一个元素的值保存在__value，并将根元素的值移动到最后一个元素
  //然后将--last，也就是说，我们这里构造了一个更小的堆，并且只是根元素有问题。
  //那么我们剩下的就是调整这个小堆。
  __adjust_heap(__first, _Distance(0), _Distance(__last - __first), __value);
}

template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__adjust_heap(_RandomAccessIterator __first, _Distance __holeIndex,
              _Distance __len, _Tp __value)
{
  _Distance __topIndex = __holeIndex;
  _Distance __secondChild = 2 * __holeIndex + 2; //找到hole节点的右子节点
  while (__secondChild < __len) {
    if (*(__first + __secondChild) < *(__first + (__secondChild - 1)))
      __secondChild--;// __secondChild指向最大的子节点。
    *(__first + __holeIndex) = *(__first + __secondChild);
    //这里SGI STL并没有和我们的__value比较大小，所以，我们这里得到的holeIndex可能是错误的。或者说只是一
    //个大概的位置。（很多优化的算法，并不是一次性完成的，而是去分情况或是其他什么的多种复合）。
    //这里可能是SGI STL在这里优化，侯捷大师，似乎在这里打个一个盹。
    __holeIndex = __secondChild;
    __secondChild = 2 * (__secondChild + 1);
  }
  if (__secondChild == __len) {//当我们的根节点没有右节点时，就搞他左边的兄弟。
    *(__first + __holeIndex) = *(__first + (__secondChild - 1));
    __holeIndex = __secondChild - 1;
  }
  //侯捷大师注 ："将与调整值添入目前洞号内，注意，此时肯定满足次序特性"
  //“依侯捷之见，下面直接改为 *(__first + __holeIndex) = value;应该可以”
  //我这里认为侯捷大师在这里打盹了，这句话如果改了的话，整个过程就出错了。
  //之前的优化，可以减少一些不必要的比较次数。但是如果把这个也省了。结果不能保证正确。
  //我们的结果不一定满足次序特性。
  __push_heap(__first, __holeIndex, __topIndex, __value);
}

比如如下例子。

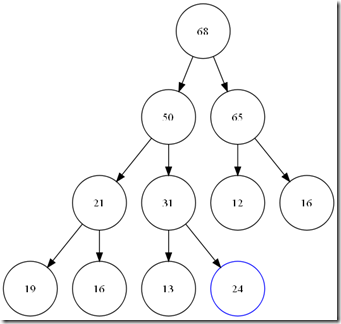
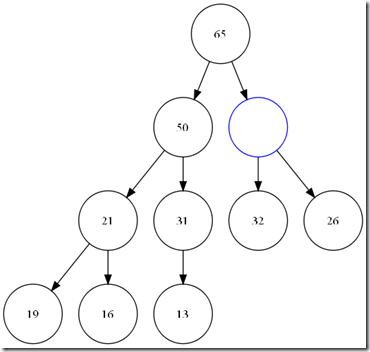
alt text

当push_heap的时候，如果直接*(first + holeIndex) = VALUE,那么就会成为这个样子。

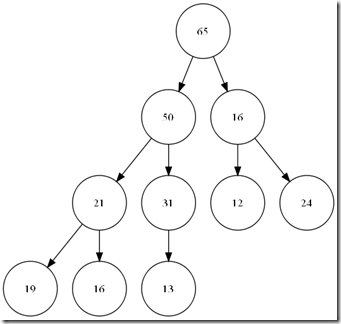
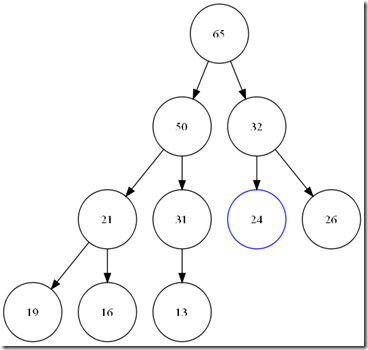
alt text

　　所以，必须要再一次经过__push_heap，再一次修正 24->16->65这条路径。保证真正的顺序。

而SGI这样实现是为了减少一些不必要的比较。

Sort_heap 　　在搞定这些基本操作之后，我们发现，我们只需要执行一次次的pop_heap，我们就可以把数据按照一定的顺序跑列出来。而这也就是堆排序。

template <class _RandomAccessIterator>

void sort_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)

{

while (__last - __first > 1)

pop_heap(__first, __last--);

}

　　我们发现，每一次pop_heap操作是O(logN)。整个数列排序结果是O(n*logN)。这已经达到比较方法的极限。而且是原地排序，而且最坏情况依然不变。heap sort的确是一个非常出色的算法。

哦，扯了这么多，我们heap的好处不少，可是如何构造heap呢？

Make_heap 　　还记得adjust_heap，这个函数，可以在左右子树满足条件情况下调整树，那么我们完全可以从下到上逐渐构造成一个符合我们要求的树。而且，树的叶子节点是没有孩子的。所以，我们可以更快的只是从中间开始。初略的估算下，每一次adjust_heap，O(logN)，一半的节点，O(n*logN)，但其实我们可以做的更快。建堆的复杂度可以达到O(n)的线性。

template <class _RandomAccessIterator>
inline void
make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
  __make_heap(__first, __last,
              __VALUE_TYPE(__first), __DISTANCE_TYPE(__first));
}

template <class _RandomAccessIterator, class _Tp, class _Distance>
void
__make_heap(_RandomAccessIterator __first,
            _RandomAccessIterator __last, _Tp*, _Distance*)
{
  if (__last - __first < 2) return;//当长度小于等于1时，我们就不需要排序了。
  _Distance __len = __last - __first;
  _Distance __parent = (__len - 2)/2;//找到第一个非叶子节点。

  while (true) {
    __adjust_heap(__first, __parent, __len, _Tp(*(__first + __parent)));
    if (__parent == 0) return;
    __parent--;
  }
}

不会开机的男孩

Comments